Déductif vs. Inductif

Raisonnement déductif Utilise des informations, des locaux ou des règles générales acceptées pour parvenir à une conclusion prouvée. D'autre part, logique inductive ou le raisonnement implique de faire des généralisations en fonction du comportement observé dans des cas spécifiques. Les arguments déductifs sont valides ou invalides. Mais la logique inductive permet aux conclusions de se tromper même si les locaux sur lesquels il est basé sont corrects. Les arguments inductifs sont donc forts ou faibles.

Tableau de comparaison

Graphique de comparaison déductive versus inductive

	Déductif	Inductif
Introduction (de Wikipedia)	Le raisonnement déductif, également appelé logique déductive, est le processus de raisonnement d'une ou plusieurs déclarations générales concernant ce qui est connu pour parvenir à une conclusion logiquement certaine.	Raisonnement inductif, également appelé induction ou logique ascendante, construit ou évalue les propositions générales dérivées d'exemples spécifiques.
Arguments	Les arguments en logique déductive sont soit valides ou invalides. Les arguments non valides ne sont toujours pas liés. Les arguments valides ne sont solides que si les locaux sur lesquels ils sont basés sont vrais.	Les arguments en raisonnement inductif sont soit forts ou faibles. Les arguments faibles sont toujours invalides. Les arguments solides ne sont convaincants que si les locaux sur lesquels ils sont basés sont vrais.
Validité des conclusions	Les conclusions peuvent être prouvées comme étant valables si les locaux sont connus pour être vrais.	Les conclusions peuvent être incorrectes même si l'argument est fort et que les locaux sont vrais.

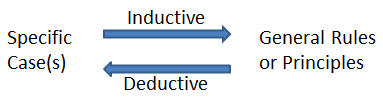Le raisonnement déductif applique des règles générales pour tirer des conclusions sur des cas spécifiques. Le raisonnement inductif observe que les modèles dans des cas spécifiques à déduire les conclusions sur les règles générales.

Par exemple: tous les hommes sont mortels. John est un homme. Par conséquent, John est mortel. Ceci est un exemple de raisonnement déductif valide. D'un autre côté, voici un exemple de raisonnement inductif: la plupart des hommes sont droitiers. John est un homme. Par conséquent, John doit être droitier. La force de cet argument inductif dépend du pourcentage de gauchers dans la population. Dans tous les cas, la conclusion pourrait bien être invalide parce que le raisonnement inductif ne garantit pas la validité des conclusions.

Qu'est-ce que le raisonnement déductif?

Le raisonnement déductif (logique descendante) contraste avec le raisonnement inductif (logique ascendante) et commence généralement par une ou plusieurs déclarations ou prémisses générales pour parvenir à une conclusion logique. Si les locaux sont vrais, la conclusion doit être valide. La résasonage déductif est utilisée par les scientifiques et les mathématiciens pour prouver leurs hypothèses.

Arguments sonores ou non liés

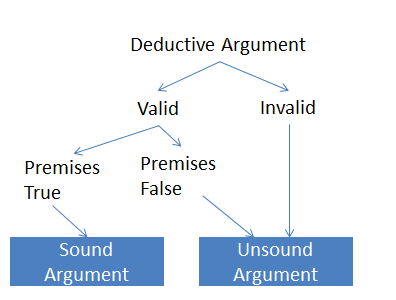
Avec un raisonnement déductif, les arguments peuvent être valides ou invalides, sonores ou non liés. Si la logique est correcte, je.e. La conclusion circule dans les locaux, puis les arguments sont valides. Cependant, des arguments valides peuvent être solides ou non liés. Si les locaux utilisés dans l'argument valide sont vrais, alors l'argument est solide sinon il n'est pas lié.

Par exemple,

1. Tous les hommes ont dix doigts.
2. John est un homme.
3. Par conséquent, John a dix doigts.

Cet argument est logique et valide. Cependant, la prémisse "Tous les hommes ont dix doigts."est incorrect parce que certaines personnes naissent avec 11 doigts. Par conséquent, c'est un argument non solide. Notez que tous les arguments non valides ne sont pas non liés.

Types de logique déductive

Loi de détachement

Une seule déclaration conditionnelle est faite et une hypothèse (p) est indiquée. La conclusion (q) est ensuite déduite de l'énoncé et de l'hypothèse. Par exemple, en utilisant la loi du détachement sous la forme d'une déclaration if-then: (1.) Si un angle a> 90 °, alors a est un angle obtus. (2.) A = 125 °. (3.) Par conséquent, A est un angle obtus.

La loi du syllogisme

La loi du syllogisme prend deux déclarations conditionnelles et constitue une conclusion en combinant l'hypothèse d'une déclaration avec la conclusion d'un autre. Par exemple, (1.) Si les freins échouent, la voiture ne s'arrêtera pas. (2.) Si la voiture ne s'arrête pas, il y aura un accident. (3.) Par conséquent, si les freins échouent, il y aura un accident.

Nous avons déduit la déclaration finale en combinant l'hypothèse de la première déclaration avec la conclusion de la deuxième déclaration.

Qu'est-ce que le raisonnement inductif?

Un raisonnement inductif, ou induction, est le raisonnement d'un cas ou de cas spécifique et de dériver une règle générale. Ceci est contre la méthode scientifique. Il fait des généralisations en observant les modèles et en dessinant des inférences qui pourraient bien être incorrectes.

Arguments convaincants et inagents

De forts arguments sont ceux où si la prémisse est vraie, la conclusion est très probablement vraie. Inversement, les arguments inductifs faibles sont tels qu'ils peuvent être faux même si les locaux sur lesquels ils sont basés sont vrais.

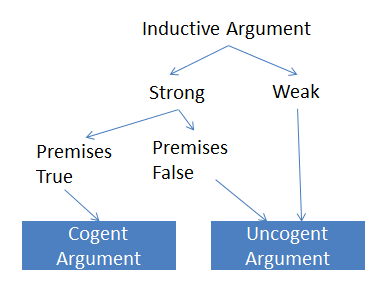
Si l'argument est solide et les locaux sur lesquels il est basé est vrai, alors il est dit être un argument convaincant. Si l'argument est faible ou si les locaux qui s'écoulent sont faux ou non prouvés, alors l'argument est dit invalide.

Par exemple, voici un exemple d'un argument fort.

1. Il y a 20 tasses de glaces dans le congélateur.
2. 18 d'entre eux sont à la vanille.
3. Par conséquent, toutes les tasses de glace sont de la vanille.

Si dans la prémisse d'argument précédente # 2 était que 2 des tasses sont de la vanille, alors la conclusion que toutes les tasses sont de la vanille seraient basées sur un argument faible. Dans les deux cas, tous les locaux sont vrais et la conclusion peut être incorrecte, mais la force de l'argument varie.

Types de raisonnement inductif

Généralisation

Une généralisation provient d'une prémisse sur un échantillon à une conclusion sur la population. Par exemple, (1.) Un échantillon de la population p est choisi. Q Pourcentage de l'échantillon S a attribué un. (2.) Par conséquent, le pourcentage Q de la population P a attribué un.

Syllogismes statistiques

Un syllogisme statistique procède d'une généralisation à une conclusion sur un individu. Par exemple, (1.) Une proportion Q de la population P a attribué un. (2.) Un individu x est membre de P. (3.) Par conséquent, il y a une probabilité qui correspond à Q que x a un attribut un.

Plus d'exemples

Exemples de raisonnement déductif

ABCD quadrilatéral a des côtés AB LL CD (parallèle) et les côtés BC LL AD. Prouver que c'est un parallélogramme. Afin de le prouver, nous devons utiliser les déclarations générales données sur le quadrilatère et parvenir à une conclusion logique.

Un autre exemple de logique déductive est le raisonnement suivant:

1. Tous les retrievers du Labrador sont des chiens.
2. Certains retrievers du Labrador sont des animaux de compagnie.
3. Par conséquent, certains chiens sont des animaux.

Exemples de raisonnement inductif

Si les trois formes consécutives sont le triangle, le carré et le pentagone qui seraient la forme suivante? Si le raisonnement observe le schéma, elle observera que le nombre de côtés dans la forme augmente de l'un et donc une généralisation de ce modèle l'amènerait à conclure que la forme suivante dans la séquence serait un hexagone.

Applications du raisonnement inductif et déductif

• La déduction peut également être temporairement utilisée pour tester une induction en l'appliquant ailleurs.
• Une bonne loi scientifique est très généralisée comme celle dans un raisonnement inductif et peut être appliquée dans de nombreuses situations pour expliquer d'autres phénomènes.
• Le raisonnement déductif est utilisé pour déduire de nombreuses expériences et prouver une règle générale.

Biais

Le raisonnement inductif est également connu sous le nom de construction d'hypothèses car toutes les conclusions faites sont basées sur les connaissances et les prédictions actuelles. Comme pour les arguments déductifs, les biais peuvent déformer l'application appropriée de l'argument inductif, ce qui empêche le raisonnement de former la conclusion la plus logique basée sur les indices.

Disponibilité heuristique

L'heuristique de disponibilité fait dépenser le raisonnement principalement des informations qui sont facilement disponibles. Les gens ont tendance à s'appuyer sur des informations facilement accessibles dans le monde qui les entoure. Cela peut introduire un biais dans le raisonnement inductif.

Biais de confirmation

Le biais de confirmation est basé sur la tendance naturelle à confirmer, plutôt que de nier une hypothèse actuelle. Par exemple, pendant plusieurs siècles, on croyait que le soleil et les planètes orbitent la terre.