Différence entre ancova et régression

ANCOVA - Variation de partitionnement

Ancova vs. Régression

L'ANCOVA et la régression sont des techniques et des outils statistiques. L'ANCOVA et la régression partagent de nombreuses similitudes, mais ont également des caractéristiques distinctives. L'ANCOVA et la régression sont basées sur une covariable, qui est une variable prédictive continue.

ANCOVA signifie analyse de la covariance. Il s'agit d'une combinaison de l'ANOVA unidirectionnelle (analyse de la variance) et de la régression linéaire, une variante de régression. Il traite des variables catégorielles et continues. Il s'agit d'une méthode statistique spécifique pour déterminer l'étendue de la variance d'une variable qui est due à la variabilité d'une autre variable.

ANCOVA est essentiellement ANOVA avec plus de sophistication et l'ajout d'une variable continue à un modèle ANOVA existant. Une autre forme d'ANCOVA est mancova (analyse multivariée de la covariance). De plus, ANCOVA est un modèle linéaire général qui a une variable de résultat continue et deux ou plusieurs variables prédictives. Les deux variables prédictives sont à la fois des variables continues et catégorielles.

Dans une variable continue, les données sont quantitatives et mises à l'échelle, tandis que les données catégorielles sont caractérisées comme nominales et non à l'échelle. ANCOVA est principalement utilisé pour contrôler les facteurs qui ne peuvent pas être randomisés mais peuvent toujours être calculés sur une échelle d'intervalle dans les conceptions expérimentales, tandis que sur les conceptions d'observation, il est utilisé pour effacer les effets variables qui modifient la relation entre les indépendants catégoriques et les personnes à charge d'intervalle. MANCOVA a également une certaine utilisation dans des modèles de régression où sa fonction principale est de s'adapter aux régressions dans les indépendants catégoriels et intervalles.

ANCOVA est un modèle qui repose sur la régression linéaire dans laquelle la variable dépendante doit être linéaire à la variable indépendante. Les origines de mancova ainsi que de l'ANOVA proviennent de l'agriculture, où les principales variables concernent les rendements des cultures.

D'un autre côté, la régression est également un outil statistique disponible dans de nombreuses variantes. Ces variantes incluent le modèle de régression linéaire, la régression linéaire simple, la régression logistique, la régression non linéaire, la régression non paramétrique, la régression robuste et la régression par étapes. La régression traite des variables continues.

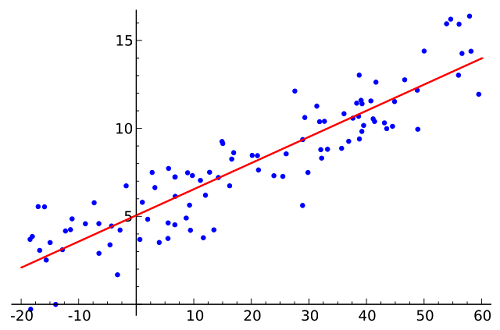
Régression linéaire

La régression est la relation d'une variable dépendante et d'une variable indépendante. Dans ce modèle, il existe une variable dépendante et une ou plusieurs variables indépendantes. Il existe également un effort pour comprendre le changement des valeurs de la variable dépendante en raison des changements dans l'une des variantes indépendantes. Dans cette situation, les autres variantes indépendantes restent fixes.

En régression, il existe deux types de base: la régression linéaire et la régression multiple. Dans la régression linéaire, la seule variable indépendante est utilisée pour expliquer et / ou prédire le résultat de «y» (que la variable essaie de prédire). D'un autre côté, il y a aussi le multiple, dans lequel la régression utilise non pas une mais deux variables indépendantes ou plus pour prédire le résultat.

L'équation pour la régression linéaire et linéaire est: y = a + bx + u, tandis que la forme pour la régression multiple est: y = a + b1x1 + b2x2 + b3x3 +… + btxt + u.

Dans les deux équations, le «Y» représente la variable que nous essayons de prévoir; Le «X» est l'outil variable pour prédire la variable «Y»; «A» est l'ordonnée, «b» est la pente, et «u» sert de résidus de régression. Il convient de noter que l'interception, la pente et le résidu de régression sont constants.

La régression est la méthode de prévision et de prédiction d'un résultat continu. C'est la méthode à utiliser pour le résultat continu, et il est basé sur une ou plusieurs variables prédictives continues. La régression a commencé à partir du domaine de la géographie dont le but est de tenter de trouver la vraie taille de la terre.

Résumé:

1.ANCOVA est un modèle linéaire spécifique en statistique. La régression est également un outil statistique, mais c'est un terme parapluie pour une multitude de modèles de régression. La régression est également le nom de l'état des relations.
2.ANCOVA traite des variables à la fois continues et catégoriques, tandis que la régression ne traite que des variables continues.
3.L'ANCOVA et la régression partagent un modèle particulier - le modèle de régression linéaire.
4.ANCOVA et la régression peuvent être effectuées à l'aide d'un logiciel spécialisé pour effectuer les calculs réels.
5.ANCOVA est venue du domaine de l'agriculture, tandis que la régression provient de l'étude de la géographie.