Différence entre l'ASA et l'AAS

ASA vs AAS: ASA représente «l'angle, le côté, l'angle», tandis que AAS signifie «angle, angle, côté»

La géométrie est amusante. La géométrie est une question de formes, de tailles et de dimensions. La géométrie est le genre de mathématiques qui traite de l'étude des formes. Il est facile de voir pourquoi la géométrie a tant d'applications qui se rapportent à la vie réelle. Il est utilisé dans tout - dans l'ingénierie, l'architecture, l'art, les sports et bien plus encore. Aujourd'hui, nous discuterons de la géométrie du triangle, en particulier la congruence du triangle. Mais d'abord, nous devons comprendre ce que signifie être congruent. Deux chiffres sont congruents si l'un peut être déplacé sur l'autre de telle manière que toutes leurs parties coïncident. En d'autres termes, deux chiffres sont appelés congruents s'ils sont de la même forme et de la même taille. Deux personnages congruents sont une et même figure, dans deux endroits différents.

C'est vrai que la congruence de Triangle est le bloc de construction de base pour de nombreux concepts et épreuves géométriques. La congruence du triangle est l'un des concepts géométriques les plus courants dans les études du secondaire. Un concept majeur souvent négligé dans l'enseignement et l'apprentissage de la congruence du triangle est le concept de suffisance, c'est-à-dire pour déterminer les conditions qui satisfont que les deux triangles sont congruents. Il y a cinq façons de déterminer si deux triangles sont congruents, mais nous allons en discuter seulement deux, c'est-à-dire ASA et AAS. ASA représente «l'angle, le côté, l'angle», tandis que l'AAS signifie «angle, angle, côté». Jetons un coup d'œil à utiliser les deux pour déterminer si deux triangles sont congruents.

Qu'est-ce que la congruence Asa Triangle?

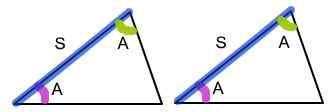
ASA signifie «angle, côté, angle», ce qui signifie que deux triangles sont congruents s'ils ont un côté égal contenu entre les angles égaux correspondants. Si les sommets de deux triangles sont en correspondance individuelle de telle sorte que deux angles et le côté inclus d'un triangle sont congruents, respectivement, aux deux angles et le côté inclus des deuxième triangles, alors il satisfait la condition que la condition que la condition que la condition que la condition soit la condition que la condition de la condition que la condition de la condition que la condition de la condition, det la condition le Les triangles sont congruents. Parce que les deux angles et le côté inclus sont égaux dans les deux triangles, les triangles sont appelés congrus.

Qu'est-ce que la congruence du triangle AAS?

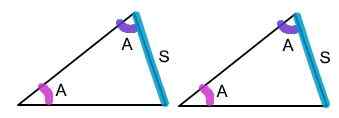
AAS signifie «angle, angle, côté», ce qui signifie deux angles et un côté opposé. AAS est l'une des cinq façons de déterminer si deux triangles sont congruents. Il indique que si les sommets de deux triangles sont en correspondance individuelle de telle sorte que deux angles et le côté opposé à l'un d'eux dans un triangle sont conformes aux angles correspondants et au côté non inclus du deuxième triangle, alors Les triangles sont congruents. Le côté non include est le côté opposé à l'un des deux angles utilisés. En termes simples, si deux paires d'angles correspondants et les côtés en face d'eux sont égaux dans les deux triangles, les deux triangles sont congruents.

Différence entre l'ASA et l'AAS

Terminologie de l'ASA et des AAS

- ASA et AAS sont deux postulats qui nous aident à déterminer si deux triangles sont congruents. ASA représente «l'angle, le côté, l'angle», tandis que l'AAS signifie «angle, angle, côté». Deux chiffres sont congruents s'ils sont de la même forme et de la même taille. En d'autres termes, deux figures congruentes sont une et même figure, à deux endroits différents. Bien que les deux soient les termes de géométrie utilisés dans les épreuves et qu'ils se rapportent au placement des angles et des côtés, la différence réside quand les utiliser. L'ASA fait référence à deux angles et à l'équipe incluse, tandis que l'AAS fait référence aux deux angles correspondants et au côté non inclus.

Congruence

- Selon la congruence de l'ASA, deux triangles sont congruents s'ils ont un côté égal contenu entre les angles égaux correspondants. En d'autres termes, si deux angles et un côté inclus d'un triangle sont égaux aux angles correspondants et au côté inclus du deuxième triangle, alors les deux triangles sont appelés congruents, selon la règle de l'ASA. La règle AAS, en revanche, indique que si les sommets de deux triangles sont en correspondance individuelle de telle sorte que deux angles et le côté opposé à l'un d'eux en un triangle sont égaux aux angles correspondants et au non côté inclus du deuxième triangle, puis les triangles sont congruents.

Représentation

- La principale différence entre les deux règles de congruence est que le côté est inclus dans le postulat ASA, tandis que le côté n'est pas inclus dans le postulat AAS.

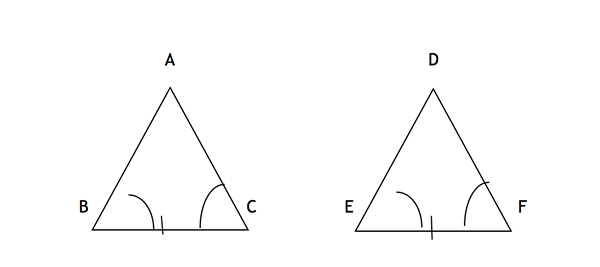
Ici, deux angles (ABC et ACB) et le côté inclus (BC) sont conformes aux angles correspondants (DEF et DFE) et un côté inclus (EF), ce qui rend les deux triangles congruents, selon la règle de congruence ASA.

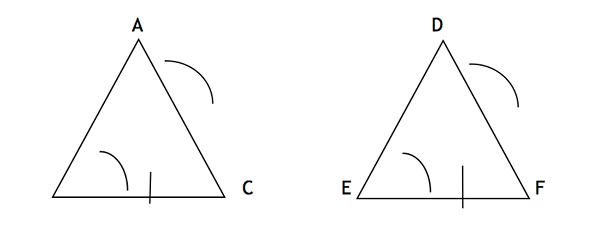
Ici, deux angles (ABC et BAC) et un côté non inclus (BC) du premier triangle sont conformes aux angles correspondants (DEF et EDF) et le côté non inclus (EF) du deuxième triangle, ce qui fait le deux triangles congruents. AC et EF peuvent également être les côtés non inclus des deux triangles respectivement.

Asa vs. AAS: tableau de comparaison

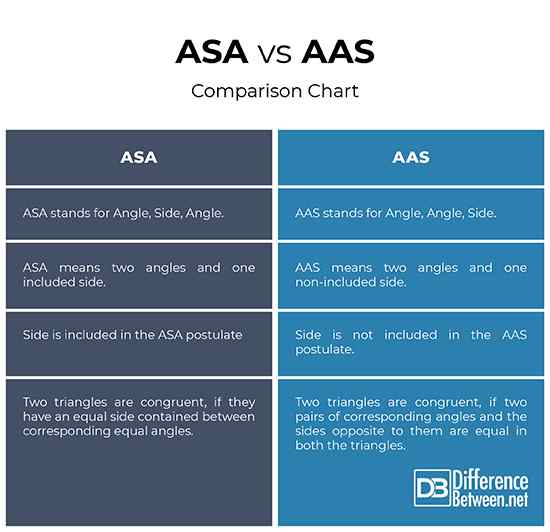
Résumé de l'ASA vs. AAS

En un mot, ASA et AAS sont deux des cinq règles de congruence qui déterminent si deux triangles sont congruents. ASA signifie «angle, côté, angle», ce qui signifie que deux triangles sont congruents s'ils ont un côté égal contenu entre les angles égaux correspondants. AAS fait référence à «l'angle, l'angle, le côté», ce qui signifie que si deux paires d'angles correspondants et les côtés en face sont égaux dans les deux triangles, les deux triangles sont appelés congruents. Bien que les deux soient essentiellement les mêmes, la principale différence entre les deux règles de congruence est que le côté est inclus dans la règle ASA, tandis que le côté n'est pas inclus dans la règle AAS.