Différence entre la distribution binomiale et de Poisson

- 3758
- 68
- Justine Dumas
 Le distribution binomiale est un, dont le nombre possible de résultats est deux, je.e. succès ou échec. D'un autre côté, il n'y a pas de limite de résultats possibles dans Distribution de Poisson
Le distribution binomiale est un, dont le nombre possible de résultats est deux, je.e. succès ou échec. D'un autre côté, il n'y a pas de limite de résultats possibles dans Distribution de Poisson
La distribution de probabilité théorique est définie comme une fonction qui attribue une probabilité à chaque résultat possible de l'expérience statistique. La distribution de probabilité peut être discrète ou continue, où, dans la variable aléatoire discrète, la probabilité totale est allouée à différents points de masse tandis que dans la variable aléatoire continue, la probabilité est distribuée à divers intervalles de classe.
La distribution binomiale et la distribution de Poisson sont deux distributions de probabilité discrètes. La distribution normale, la distribution étudiante, la distribution du chi carré et la distribution F sont les types de variables aléatoires continues. Donc, nous y allons discuter de la différence entre la distribution binomiale et de Poisson. Regarde.
Contenu: Distribution binomiale vs Distribution de Poisson
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Distribution binomiale | Distribution de Poisson |
|---|---|---|
| Signification | La distribution binomiale est celle dans laquelle la probabilité de nombre répété d'essais est étudié. | La distribution de Poisson donne le nombre d'événements indépendants se produit au hasard avec une période de temps donnée. |
| Nature | Biaparamétrique | Uniparamétrique |
| Nombre de procès | Fixé | Infini |
| Succès | Probabilité constante | Chance infinitésimale de succès |
| Résultats | Seulement deux résultats possibles, je.e. succès ou échec. | Nombre illimité de résultats possibles. |
| Moyenne et variance | Moyenne> variance | Moyenne = variance |
| Exemple | Expérience de lancement de pièces. | Impression des erreurs / page d'un grand livre. |
Définition de la distribution binomiale
La distribution binomiale est la distribution de probabilité largement utilisée, dérivée du processus de Bernoulli (une expérience aléatoire nommée d'après un mathématicien renommé Bernoulli). Il est également connu sous le nom de distribution biparamétrique, car il est présenté par deux paramètres n et p. Ici, n est les essais répétés et P est la probabilité de succès. Si la valeur de ces deux paramètres est connue, cela signifie que la distribution est pleinement connue. La moyenne et la variance de la distribution binomiale sont indiquées par µ = np et σ2 = npq.
P (x = x) = nCX pX qn-x, x = 0,1,2,3… n
= 0, sinon
Une tentative de produire un résultat particulier, qui n'est pas du tout certain et impossible, est appelé un procès. Les essais sont indépendants et un entier positif fixe. Il est lié à deux événements mutuellement exclusifs et exhaustifs; dans lequel l'occurrence est appelée succès et non-occurrence est appelée échec. P représente la probabilité de succès tandis que Q = 1 - P représente la probabilité d'échec, qui ne change pas tout au long du processus.
Définition de la distribution de Poisson
À la fin des années 1830, un célèbre mathématicien français Simon Denis Poisson a présenté cette distribution. Il décrit la probabilité que le nombre d'événements se produise dans un intervalle de temps fixe. C'est une distribution uniparamétrique car il est présenté par un seul paramètre λ ou m. Dans la distribution de Poisson, la moyenne est notée par m i.e. µ = m ou λ et la variance est étiquetée comme σ2 = m ou λ. La fonction de masse de probabilité de x est représentée par:
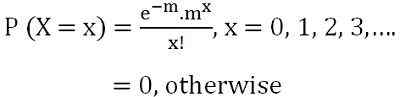 où e = quantité transcendantale, dont la valeur approximative est 2.71828
où e = quantité transcendantale, dont la valeur approximative est 2.71828
Lorsque le nombre de l'événement est élevé mais que la probabilité de son occurrence est assez faible, la distribution de Poisson est appliquée. Comme par exemple, le nombre de réclamations d'assurance / jour sur une compagnie d'assurance.
Différences clés entre la distribution binomiale et de Poisson
Les différences entre la distribution binomiale et de Poisson peuvent être clairement établies sur les motifs suivants:
- La distribution binomiale est celle dans laquelle la probabilité de nombre répété d'essais est étudié. Une distribution de probabilité qui donne le décompte d'un certain nombre d'événements indépendants se produisent au hasard dans une période donnée, est appelée distribution de probabilité.
- La distribution binomiale est biparamétrique, i.e. Il est présenté par deux paramètres N et P alors que la distribution de Poisson est uniparamétrique, i.e. caractérisé par un seul paramètre m.
- Il y a un nombre fixe de tentatives dans la distribution binomiale. D'un autre côté, un nombre illimité d'essais sont là dans une distribution de Poisson.
- La probabilité de succès est constante dans la distribution binomiale mais dans la distribution de Poisson, il y a un nombre extrêmement faible de chances de succès.
- Dans une distribution binomiale, il n'y a que deux résultats possibles, je.e. succès ou échec. Inversement, il y a un nombre illimité de résultats possibles dans le cas de la distribution de Poisson.
- Dans la distribution binomiale moyenne> variance tandis que dans la distribution de Poisson moyenne = variance.
Conclusion
Outre les différences ci-dessus, il existe un certain nombre d'aspects similaires entre ces deux distributions I.e. Les deux sont la distribution de probabilité théorique discrète. De plus, sur la base des valeurs des paramètres, les deux peuvent être unimodaux ou bimodaux. De plus, la distribution binomiale peut être approximée par la distribution de Poisson, si le nombre de tentatives (n) tend à l'infini et à la probabilité de réussite (P) tend à 0 de sorte que m = np.
- « Différence entre statistique et paramètre
- Différence entre la méthode de la mise en commun des intérêts et la méthode d'achat »

