Différence entre cercle et sphère
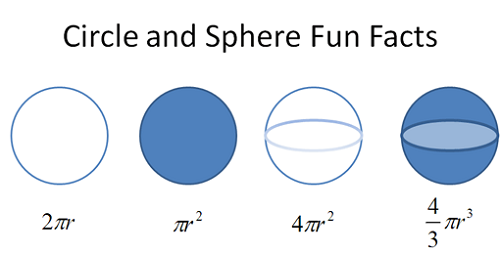
- 961
- 224
- Anaïs Fournier
La Terre sur laquelle nous vivons peut nous rappeler un cercle, mais pas entièrement parfait, et sa «zone sur laquelle la population humaine est située, dans ce cas, peut être identifiée avec une sphère. Par conséquent, la géométrie des cercles et des sphères a sa large application dans tous les domaines de la science, à partir de, comme exemple - en géographie, géologie et géodésie. Des formes sphériques peuvent en effet être trouvées à divers endroits dans la nature, et en raison de la curiosité humaine, il y a un besoin de leur description.
Qu'est-ce que le cercle?
Une ligne circulaire est un ensemble de points dans un plan avec la propriété que tous les points de cette ligne sont à une distance égale r d'un point fixe de cet avion appelé le centre de la ligne circulaire. Chaque ligne qui relie le centre avec un point de la ligne circulaire est appelée rayon, et le nombre r est la longueur du rayon de cette ligne circulaire. Dans la littérature, le terme cercle est probablement, le plus souvent utilisé. Un cercle est un cas particulier d'ellipse. L'ellipse peut être défini comme une figure géométrique des points du plan avec une somme constante de distances entre deux points fixes. En cas de cercle, ces deux points (centre et focus) sont les mêmes. Il est connu que chaque cercle a un ensemble unique de trois points qui ne se trouvent pas dans la même direction. Ces points définissent les bords du triangle, et le centre du cercle circonscrit de ce triangle se trouve dans la section transversale des lignes de bissection. La distance entre le centre et l'un des trois points donnés est le rayon du cercle. Une autre façon de déterminer un cercle à travers trois points est d'écrire l'équation de forme générale du cercle, sous forme canonique (standard) ou de pente de point, pour inclure les coordonnées des points donnés et résoudre le système. La zone d'un cercle donné avec un rayon R est égale à πr2.
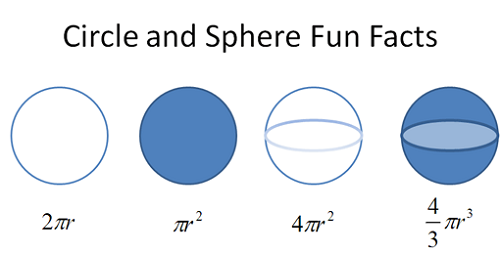
Qu'est-ce que la sphère?
Un espace peut être considéré comme un ensemble de points appelés éléments de l'espace. Une balle est un corps géométrique qui est un sous-ensemble d'un espace. C'est un ensemble de points d'un avion qui se trouvent sur une certaine distance (longueur) d'un point fixe O. Le point O est le centre de la sphère, et la longueur qui relie le centre au point le plus éloigné de la sphère est appelée un rayon. Le diamètre est la ligne qui relie deux points de bord les plus éloignés (la plus longue ligne droite) de la sphère et passe par son centre. Un cercle formé par l'intersection de la sphère et de l'avion passant par le centre de la sphère est appelé le grand cercle de la sphère. Tous les autres cercles formés par l'intersection du plan et de la sphère sont appelés petits cercles de la sphère. À travers chaque ensemble de trois points de la sphère, il n'y a qu'un seul cercle qui lui appartient.
- La zone d'une sphère est 4πr2;
- Le volume d'une sphère est 4/3πr3;
Différence entre cercle et sphère
- Définition
Un cercle est une ligne courbe fermée. Chaque point de cette ligne incurvée est sur la même distance du point focal (centre) du cercle. Le lieu d'un point qui est à une longueur fixe d'un autre point est connu sous le nom de cercle. Le point fixe est un centre d'un cercle, et la longueur entre ces deux points son rayon. De même, une sphère est également caractérisée comme un locus d'un point qui est à une distance constante d'un point fixe - mais dans un espace tridimensionnel. En termes simples - un cercle est un objet rond dans un plan, tandis qu'une sphère est un objet rond dans un espace.
- Formules
Cercle, comme une figure bidimensionnelle n'a qu'une zone - πr2. Sphère, en revanche, comme une figure tridimensionnelle (objet) a une zone - 4πr2 et un volume - 4/3πr3.
- Exemples
Naturellement, le cercle et la sphère sont des figures qui peuvent être couramment trouvées tout autour de nous. Bien qu'un exemple réel d'un cercle soit inexistant car il n'y a pas d'objet de largeur zéro en réalité - certains objets peuvent être utilisés pour le décrire - comme les roues, les CD, les pièces. Les exemples de sphère sont peut-être plus faciles à trouver - des balles de tennis, des planètes, des oranges, des globes, etc.
Cercle vs. Sphère
| Cercle | Sphère |
| objet rond dans un plan | objet rond dans un espace |
| bidimensionnel (figure) | trois dimensions (objet) |
| seule la zone peut être calculée | Les calculs comprennent à la fois la zone et un volume |
Résumé
- Les cercles et les sphères ont une symétrie parfaite autour de leurs centres. Tous les points d'un cercle et les points les plus éloignés d'une sphère sont à une distance fixe du point focal (centre). Cependant, il y a des différences comme ce qu'un cercle est bidimensionnel, tandis qu'une sphère est un objet tridimensionnel. La distance entre les points les plus éloignées est appelée diamètre (et est le double du rayon).
- Un cercle a une zone qui peut être calculée avec la formule - πr2. Une sphère avec une zone (calculée avec la formule 4πr2) a un volume égal à 4/3πr3.
- Des exemples de vie réel d'un cercle ne peuvent pas être trouvés comme un cercle existe en tant que concept bidimensionnel - il n'a obtenu que la longueur et la hauteur et pas de largeur. Cependant, certains objets peuvent ressembler à un cercle - cookies, pizza, pneus… les exemples d'objets en forme de sphère sont le softball, les marbres, les atomes, les pommes, etc.

