Différence entre le codomaine et la plage

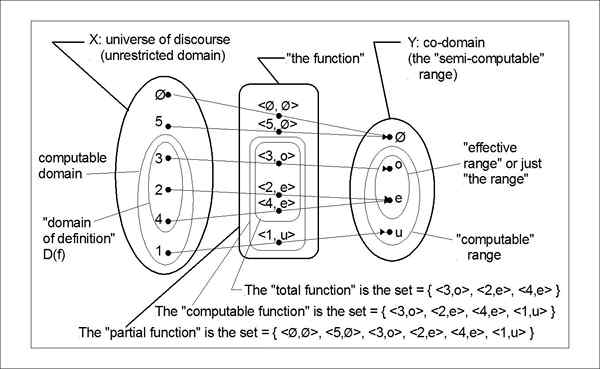
Le codomaine et la gamme sont les notions de fonctions utilisées en mathématiques. Bien que les deux soient liés à la sortie, la différence entre les deux est assez subtile. Le terme «gamme» est parfois utilisé pour se référer au «codomaine».  Lorsque vous distinguez les deux, vous pouvez vous référer au codomaine comme la sortie, la fonction est déclarée produire. La gamme de terme, cependant, est ambiguë car elle peut parfois être utilisée exactement comme le codomaine est utilisé. Prenons F: A -> b, où F est la fonction de a à b. Ensuite, B est le codomaine de la fonction "F»Et la plage est l'ensemble des valeurs que la fonction prend, qui est indiquée par F (UN). La plage peut être égale ou inférieure au codomaine mais ne peut pas être supérieure à celle.

Par exemple, que A = 1, 2, 3, 4, 5 et b = 1, 4, 8, 16, 25, 64, 125. La fonction F: A -> b est défini par F (x) = x ^ 3. Alors ici,

Domain = set a

Codomaine = set b, et

Gamme (r) = 1, 8, 64, 125

La gamme doit être le cube de l'ensemble A, mais le cube de 3 (c'est-à-dire 27) n'est pas présent dans l'ensemble B, donc nous avons 3 dans le domaine, mais nous n'en avons pas 27 dans le codomaine ou la gamme. La plage est le sous-ensemble du codomaine.

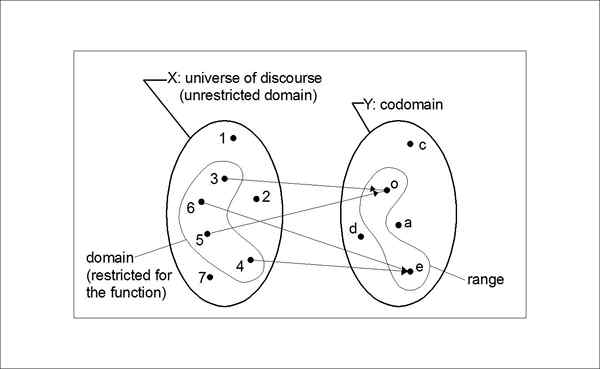
Qu'est-ce que le codomaine d'une fonction?

Le «codomaine» d'une fonction ou d'une relation est un ensemble de valeurs qui pourraient éventuellement en sortir. Cela fait en fait partie de la définition de la fonction, mais il restreint la sortie de la fonction. Par exemple, prenons la notation de la fonction F: R -> r. Cela signifie que F est une fonction des nombres réels aux nombres réels. Ici, le codomaine est l'ensemble des nombres réels R ou l'ensemble des sorties possibles qui en sortent. Le domaine est également l'ensemble des nombres réels r. Ici, vous pouvez également spécifier la fonction ou la relation pour restreindre toutes les valeurs négatives que la sortie produit. En termes simples, le codomaine est un ensemble dans lequel les valeurs d'une fonction tombent.

Soit n l'ensemble des nombres naturels et la relation est définie comme r = (x, y): y = 2x, x, y ∈ N

Ici, X et Y sont toujours des nombres naturels. Donc,

Domaine = n, et

Codomaine = n c'est l'ensemble des nombres naturels.

Quelle est la gamme d'une fonction?

La «plage» d'une fonction est appelée l'ensemble des valeurs qu'elle produit ou simplement comme l'ensemble de sortie de ses valeurs. La gamme de terme est souvent utilisée comme codomaine, cependant, dans un sens plus large, le terme est réservé au sous-ensemble du codomaine. En termes simples, la plage est l'ensemble de toutes les valeurs de sortie d'une fonction et une fonction est la correspondance entre le domaine et la plage. Dans la théorie des ensembles natifs, la plage fait référence à l'image de la fonction ou du codomaine de la fonction. Dans les mathématiques modernes, la gamme est souvent utilisée pour désigner l'image d'une fonction. Les livres plus anciens ont été référés à ce que l'on appelle actuellement le codomaine et les livres modernes utilisent généralement la gamme de terme pour se référer à ce qui est actuellement connu sous le nom d'image. La plupart des livres n'utilisent pas du tout la gamme de mots pour éviter complètement les confusions.

Par exemple, que A = 1, 2, 3, 4 et b = 1, 4, 9, 25, 64. La fonction F: A -> b est défini par F (x) = x ^ 2. Alors ici, le jeu A est le domaine et le jeu B est le codomaine, et Range = 1, 4, 9. La plage est le carré de A tel que défini par la fonction, mais le carré de 4, qui est de 16 ans, n'est pas présent dans le codomaine ni dans la plage.

Différence entre le codomaine et la plage

Définition du codomaine et de la gamme

Les deux termes sont liés à la sortie d'une fonction, mais la différence est subtile. Alors que le codomaine d'une fonction est un ensemble de valeurs qui pourraient éventuellement en sortir, elle fait en fait partie de la définition de la fonction, mais elle restreint la sortie de la fonction. La gamme d'une fonction, en revanche, fait référence à l'ensemble de valeurs qu'elle produit réellement.

Objectif du codomaine et de la gamme

Le codomaine d'une fonction est un ensemble de valeurs qui inclut la plage mais peut inclure certaines valeurs supplémentaires. Le but du codomaine est de restreindre la sortie d'une fonction. La plage peut être difficile à spécifier parfois, mais un ensemble de valeurs plus important qui incluent la plage entière peut être spécifiée. Le codomaine d'une fonction sert parfois le même objectif que la plage.

Exemple de codomaine et de plage

Si a = 1, 2, 3, 4 et b = 1, 2, 3, 4, 5, 6, 7, 8, 9 et la relation F: A -> b est défini par F (x) = x ^ 2, alors codomaine = set b = 1, 2, 3, 4, 5, 6, 7, 8, 9 et range = 1, 4, 9. La plage est le carré de l'ensemble A mais le carré de 4 (c'est-à-dire 16) n'est pas présent dans l'ensemble B (codomaine) ou la plage.

Codomaine vs. Gamme: graphique de comparaison

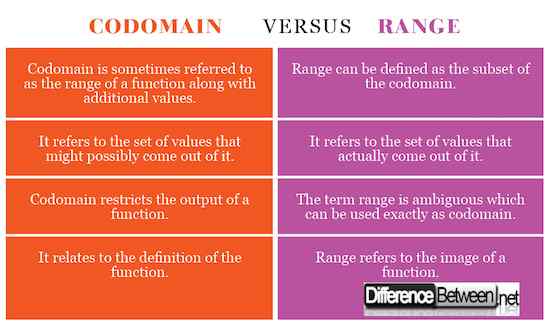
Résumé du codomaine vs. Gamme

Alors que les deux sont des termes communs utilisés dans la théorie des ensembles natifs, la différence entre les deux est assez subtile. Le codomaine d'une fonction peut être simplement appelé l'ensemble de ses valeurs de sortie possibles. En termes mathématiques, il est défini comme la sortie d'une fonction. La plage d'une fonction, en revanche, peut être définie comme l'ensemble des valeurs qui en sortent réellement. Cependant, le terme est ambigu, ce qui signifie qu'il peut être utilisé parfois exactement comme codomaine. Cependant, en mathématiques modernes, la gamme est décrite comme le sous-ensemble du codomaine, mais dans un sens beaucoup plus large.