Différence entre différenciation et intégration

Le calcul est l'une des principales applications mathématiques qui sont appliquées dans le monde aujourd'hui pour résoudre divers phénomènes. Il est hautement employé dans les études scientifiques, les études économiques, la finance et l'ingénierie parmi d'autres disciplines qui jouent un rôle vital dans la vie d'un individu. L'intégration et la différenciation sont les fondamentaux utilisés dans le calcul pour étudier le changement. Cependant, de nombreuses personnes, y compris les étudiants et les universitaires, n'ont pas été en mesure de mettre en évidence les différences entre la différenciation et l'intégration.

Qu'est-ce que la différenciation?

La différenciation est un terme utilisé dans le calcul pour se référer au changement, quelles propriétés expériences concernant un changement d'unité dans une autre propriété connexe.

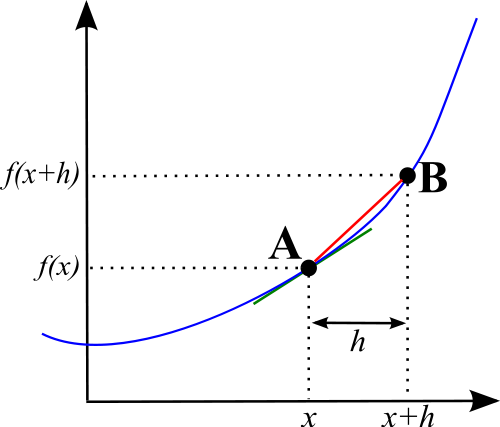
Dans un autre terme, la différenciation forme une expression algébrique qui aide à calculer le gradient d'une courbe au point donné. Il est important de souligner que les courbes ont leurs pentes variant à un point donné contrairement aux lignes droites, qui ont le même gradient tout au long.

Qu'est-ce que l'intégration?

L'intégration est un terme utilisé dans le calcul pour désigner la formule et la procédure de calcul de la zone sous la courbe.

Il convient de noter que le graphique doit être sous une courbe, ce qui résulte de la formation d'une partie intégrante, qui est difficile à trouver la zone contrairement à d'autres formes comme les cercles, les carrés et les rectangles, qui sont plus faciles à calculer leurs zones.

Différence entre différenciation et intégration

1) Objectif et fonctions de différenciation et d'intégration

L'intégration et la différenciation peuvent être principalement différenciées dans la façon dont les deux concepts sont appliqués et leurs résultats ultimes. Ils sont utilisés pour arriver à différentes réponses, qui est la différence fondamentale. La différenciation est utilisée pour calculer le gradient de la courbe. Les courbes non linéaires ont des pentes différentes à un point donné, ce qui rend difficile la détermination de leurs gradients. L'expression algébrique utilisée pour déterminer le changement engagé d'un point à un autre avec une unité est appelée différenciation.  D'un autre côté, l'intégration est une expression algébrique utilisée pour calculer la zone sous la courbe car ce n'est pas une forme parfaite après laquelle la zone peut facilement être calculée.

2) directement opposé

Les fonctions algébriques de différenciation et d'intégration sont directement opposées les unes aux autres, en particulier dans leur application. Si l'on effectue l'intégration, il ou elle montre le contraire de la différenciation tandis que si l'on effectue une différenciation, il ou elle se produit en face de l'intégration. Par exemple, l'intégration et la différenciation forment une relation qui est également représentée lorsque l'on effectue le carré d'un nombre, puis trouve la racine carrée du résultat. Par conséquent, si l'on veut trouver le contraire d'un nombre intégré, il ou elle devra effectuer la différenciation du même numéro. Simplement, l'intégration est le processus inverse de la différenciation et vice versa.

3) Application de la vie réelle pour la différenciation et l'intégration

Dans les scénarios de la vie réelle, l'intégration et la différenciation se sont révélées être appliquées différemment à chaque concept utilisé pour fournir des résultats différents. Néanmoins, il est remarquable de souligner que les deux différenciations sont des concepts de calcul essentiels qui facilitent la vie. L'une des principales applications de l'intégration est le calcul des zones des surfaces incurvées, le calcul du volume d'objets et le calcul du point central entre autres fonctions.

D'un autre côté, le concept de différenciation est considérablement utilisé pour calculer la vitesse instantanée et utilisé pour déterminer si une fonction augmente ou diminue en conséquence. Ceci est une démonstration claire de la façon dont les deux concepts sont appliqués dans la vie des individus.

4) vitesse et fonction de différenciation et d'intégration

L'autre différence entre l'intégration et la différenciation est le rôle qu'ils jouent en ce qui concerne une fonction donnée à l'étude. Selon les mathématiciens, la différenciation aide considérablement à déterminer la vitesse de la fonction en aidant au calcul de la vitesse instantanée. D'un autre côté, l'intégration concerne la détermination de la distanciation parcourue par une fonction donnée. La zone sous la courbe est estimée équivalente à la distance parcourue par la fonction. L'expression algébrique d'intégration aide à calculer la zone sous la courbe, ce qui équivaut à la distance parcourue par la fonction.

Expressions / formules algébriques pour la différenciation et l'intégration

Il convient également de noter que la différenciation et l'intégration ont différentes expressions algébriques, qui sont utilisées dans le calcul. Cela explique pourquoi les deux concepts de calcul fourniront toujours des résultats différents.  La dérivée d'une fonction f (x) concernant la variable x et selon la règle du produit sera définie comme:

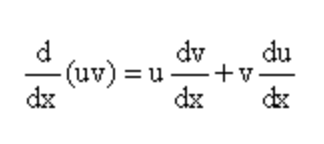
D'un autre côté, la formule d'intégration ou la zone intégrale sous la courbe peut être calculée par l'utilisation de la formule:

∫f (x) dx, qui est la formule adoptée sous la méthode de substitution.

5) Ajout et division

L'autre méthode pour comparer l'intégration à la différenciation est en expliquant spécifiquement comment chaque fonction réalise ses résultats. L'intégration détermine le résultat d'une fonction spécifique en ajoutant les aspects associés au calcul. D'un autre côté, la différenciation détermine la vitesse instantanée et la vitesse de la fonction à travers la division.

Différences entre la différenciation et l'intégration: graphique de comparaison

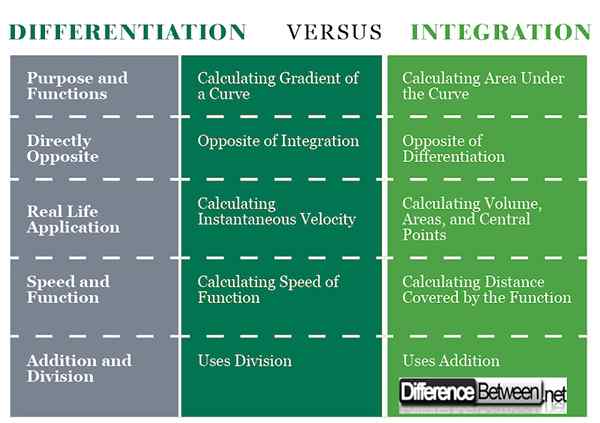
Résumé de la différenciation vs. L'intégration

• L'une des principales variations entre la différenciation et l'intégration est que les deux fonctions de calcul sont directement opposées les unes aux autres dans leur application.
• Les étudiants et autres chercheurs devraient se concentrer sur la compréhension de l'un des concepts, après quoi ils devront effectuer le contraire pour déterminer les résultats de l'autre fonction.
• La compréhension des différences qui existent entre l'intégration et la différenciation sont essentielles car elle aidera les individus à utiliser la bonne expression algébrique si nécessaire.
• Enfin, il est essentiel de maîtriser les deux concepts de calcul en mathématiques de base car ils ont toujours été utilisés dans diverses disciplines comme l'économie, les affaires et l'ingénierie.