Différence entre la dispersion et l'asymétrie

Le degré de variations est souvent exprimé en termes de données numériques à un seul but de comparaison dans la théorie et l'analyse statistiques. Nous calculons normalement un seul chiffre pour représenter l'ensemble des données, ce qui est appelé «moyenne». Cependant, il ne spécifie aucun moyen particulier de déterminer la composition de la série. En raison de quelles mesures supplémentaires sont nécessaires pour nous éclairer sur la façon dont les éléments varient les uns des autres ou autour de la moyenne. Pour comprendre les concepts très détaillés d'analyse quantitative dans les statistiques, nous utilisons des mesures de la dispersion et de l'asymétrie. La dispersion est une mesure de l'éventail de distribution autour de l'emplacement central tandis que l'asymétrie est une mesure de l'asymétrie dans une distribution statistique.

Qu'est-ce que la dispersion?

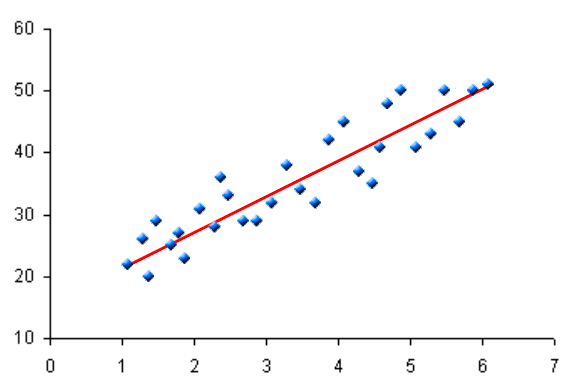
Dans les statistiques, la dispersion est une mesure de la répartition des données, ce qui signifie qu'elle spécifie comment les valeurs d'un ensemble de données diffèrent les unes des autres en taille. C'est la plage à laquelle une distribution statistique se propage autour d'un point central. Il détermine principalement la variabilité des éléments d'un ensemble de données autour de son point central. Autrement dit, il mesure le degré de variabilité autour de la valeur moyenne. Les mesures de la dispersion sont importantes pour déterminer la propagation des données autour d'une mesure de l'emplacement. Par exemple, la variance est une mesure standard de la dispersion qui spécifie comment les données sont distribuées sur la moyenne. D'autres mesures de la dispersion sont la plage et la déviation moyenne.

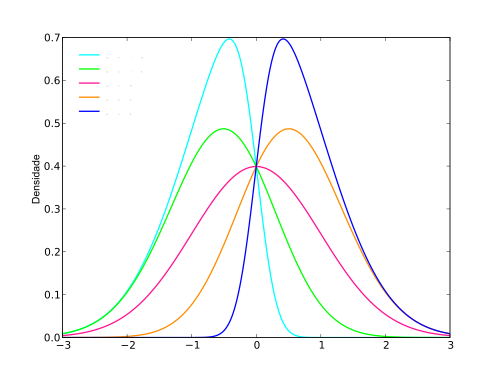
Qu'est-ce que l'asymétrie?

L'asymétrie est une mesure de l'asymétrie de la distribution sur un certain point. Une distribution peut être légèrement asymétrique, fortement asymétrique ou symétrique. La mesure de l'asymétrie d'une distribution est calculée à l'aide de l'asymétrie. En cas d'asymétrie positive, la distribution serait asymétrique et lorsque l'asymétrie est négative, la distribution serait asymétrique. Si l'asymétrie est nulle, la distribution est symétrique. L'asymétrie est mesurée sur la base de la moyenne, de la médiane et du mode. La valeur de l'asymétrie peut être positive, négative ou non définie selon que les points de données sont biaisés à gauche ou biaisés vers la droite.

Différence entre la dispersion et l'asymétrie

1. Définition de la dispersion vs. Asymétrie

En termes statistiques et théorie des probabilités, la dispersion est la taille de la plage de valeurs pour une variable aléatoire ou sa distribution de probabilité. Il décrit une plage à laquelle une distribution est étirée ou se propage. Autrement dit, c'est une mesure pour étudier la variabilité des éléments. L'asymétrie, en revanche, est une mesure de l'asymétrie dans une distribution statistique d'une variable aléatoire sur sa moyenne. La valeur de l'asymétrie peut être à la fois positive et négative, ou parfois indéfinie. En termes simples, les distributions asymétriques seraient biaisées

2. Mesures de la dispersion vs. Asymétrie

Les mesures de la dispersion signifient la mesure dans laquelle les variations sont déséquilibrées de leur valeur centrale. Plus précisément, il mesure le degré de variabilité de la valeur d'une variable autour de la valeur moyenne. La dispersion indique la propagation des données. Les mesures de l'asymétrie signifient comment est asymétrique la distribution et détermine si les points de données sont biaisés vers la droite ou vers la gauche. Si la distribution est censée être biaisée vers la gauche, alors la valeur est négative et la valeur est positive si la distribution est biaisée vers la droite.

3. Calcul de la dispersion vs. Asymétrie

La dispersion est calculée sur la base d'une certaine moyenne. Il s'agit d'un calcul statistique qui mesure le degré de variation et il existe de nombreuses façons de calculer la dispersion, mais les deux des plus courantes sont la gamme et la déviation moyenne. La plage est la différence entre la plus grande et les plus petites valeurs dans un ensemble de données, tandis que l'écart moyen est la moyenne des valeurs absolues des écarts des valeurs fonctionnelles par rapport à un point central. L'asymétrie, en revanche, est calculée sur la base de la moyenne, de la médiane et du mode. Si la moyenne est supérieure au mode, vous avez un asymétrie positif et dans le cas où la moyenne est inférieure au mode, vous avez un biais négatif. De plus, la distribution a une biais nul en cas de distribution symétrique.

4. Applications de dispersion vs. Asymétrie

La dispersion est principalement utilisée pour décrire la relation entre un ensemble de données et déterminer le degré de variation des valeurs des données de leur valeur moyenne. La dispersion statistique peut être utilisée pour d'autres méthodes statistiques telles que l'analyse de régression, qui est un processus utilisé pour comprendre la relation entre les variables. Il peut également être utilisé pour tester la fiabilité de la moyenne. L'asymétrie, en revanche, traite de la nature de la distribution dans un ensemble de données. Il est extrêmement utile en ce qui concerne l'analyse économique dans le secteur des finances qui implique un large ensemble de données telles que les rendements des actions, les cours des actions, etc.

Dispersion vs. Asymétrie: tableau de comparaison

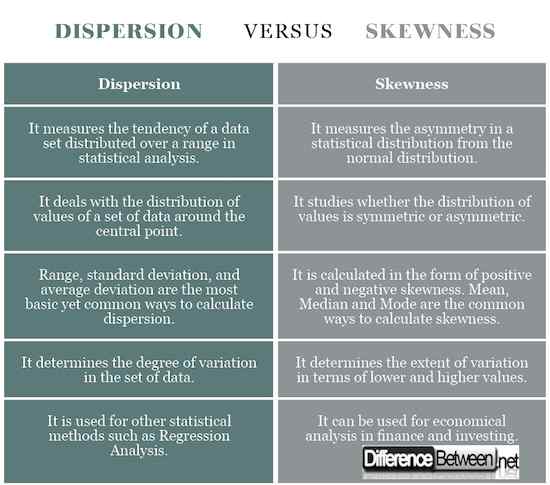
Résumé de la dispersion vs. Asymétrie

Les deux sont les termes les plus courants utilisés dans l'analyse statistique et la théorie des probabilités pour caractériser un ensemble de données impliquant une énorme masse de données numériques. La dispersion est une mesure pour calculer la variabilité des données ou étudier les variations des données entre elles ou autour de sa moyenne. Il traite principalement de la distribution des valeurs des données dans un ensemble autour de son point central. Il peut être mesuré de plusieurs façons, dont la plage et la déviation moyenne sont les plus courantes. L'asymétrie est utilisée pour mesurer l'asymétrie de la distribution normale dans un ensemble de données signifiant le degré auquel la distribution est décomposable autour de la moyenne.