Différence entre la croissance exponentielle et la décroissance exponentielle

La croissance exponentielle augmente les valeurs de façon exponentielle avec le temps tandis que la désintégration diminue exponentiellement les valeurs avec le temps.

Qu'est-ce que la croissance exponentielle?

Définition de la croissance exponentielle:

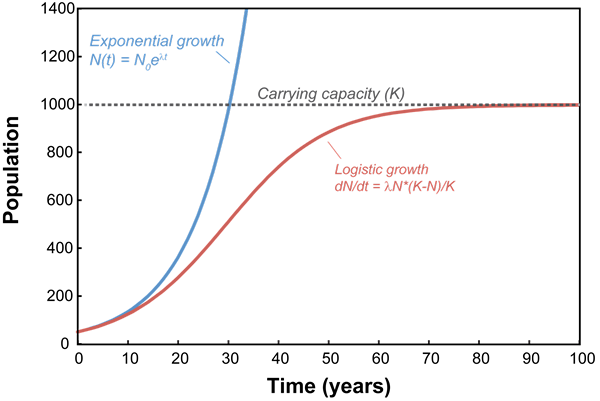
La croissance exponentielle est lorsque le nombre d'une entité augmente rapidement de manière exponentielle au fil du temps. Une fonction mathématique de croissance exponentielle est celle dans laquelle les nombres se multiplient à mesure que le temps progresse. Un exposant fait également partie de l'équation, donc par exemple, une équation pourrait être y = 5 * 2^X. Dans ce cas, chaque nombre, à partir de 5, est multiplié par 2 en une puissance d'exposant telle que 2. L'exposant est généralement un entier supérieur à 1, de sorte que lorsqu'un nombre est élevé à cette puissance, il produit un nombre encore plus grand.

Graphique pour la croissance exponentielle:

Dessiner un graphique de cette fonction produirait une ligne incurvée qui monte vers le haut. La pente changera constamment à mesure que plus de nombres sont placés dans l'équation. Pour obtenir une équation pour la pente, vous devrez calculer le dérivé en utilisant le calcul. À mesure que les nombres sur l'axe x du graphique, la variable de temps, deviennent plus grands, les nombres sur l'axe y sont également. La relation entre les variables n'est pas inverse et les pentes vers le haut.

Exemples de croissance exponentielle:

Des exemples de croissance exponentielle peuvent être observés dans les populations de bactéries qui se divisent très rapidement. Salmonella enterica Les bactéries sérovar typhimurium, par exemple, ont été largement étudiées et montrées comme ayant une phase de décalage pendant laquelle ils se préparent à entrer dans un schéma de croissance exponentielle. Les bactéries se diviseront et la population se développera de façon exponentielle jusqu'à ce qu'il ne reste plus de nutriments.

Utilisations de la croissance exponentielle:

Connaître le taux de croissance des bactéries dans diverses conditions peut être utile pour permettre aux scientifiques de développer divers agents antimicrobiens. Ces antibiotiques peuvent ensuite être testés et évalués en fonction de leur impact sur le taux de croissance exponentiel de la cible bactérienne.

Qu'est-ce que la décadence exponentielle?

Définition de la décomposition:

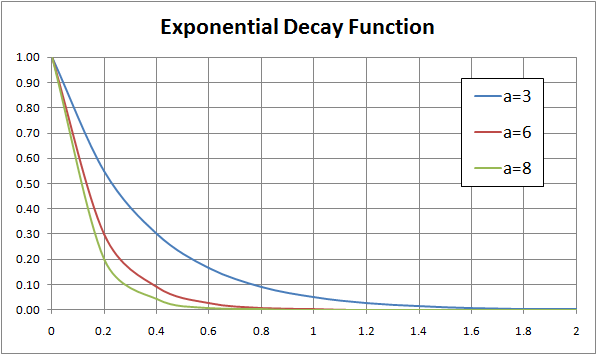
La désintégration est lorsque les nombres diminuent avec le temps de manière exponentielle, donc le résultat ressemble à une division répétée. Une équation exponentielle est toujours impliquée mais l'exposant est tel que les valeurs continuent de diminuer ou de se décomposer au fil du temps. Par exemple, disons que nous avons une équation: y = 5 * 2^X. Dans ce cas, chaque nombre, à partir de 5, est multiplié par 2 à une puissance d'exposant telle que 1/2. L'exposant est une fraction telle que les nombres diminuent en taille lorsqu'ils sont branchés sur l'équation.

Graphique:

Dessiner un graphique de cette fonction produirait une ligne incurvée qui descendait vers le bas. La pente changera constamment à mesure que plus de nombres sont placés dans l'équation. Pour obtenir une équation pour la pente, vous devrez calculer le dérivé en utilisant le calcul. À mesure que les nombres sur l'axe x du graphique, la variable de temps, deviennent plus grands pour que les nombres sur l'axe y soient, la variable de taille devient plus petite. Ceci est une relation inverse entre les deux variables du temps et de la taille, et le graphique descend vers le bas.

Exemples de désintégration exponentielle:

Un bon exemple de décroissance est la valeur d'une nouvelle voiture. Lorsque vous achetez la voiture pour la première fois, cela vaut beaucoup d'argent, mais au fil du temps, il se déprécie et perd de la valeur afin que si vous veniez la voiture, vous obtiendriez moins que vous ne l'avez payé au début. En science, la désintégration radioactive des isotopes est un bon exemple de processus naturel de décroissance qui se produit. La demi-vie d'un isotope est le temps qu'il faut à la moitié de l'atome pour se décomposer.

Les usages:

Connaître la décroissance radioactive de certains isotopes a été très utile car il a permis aux scientifiques de sortir avec des fossiles qui ont été trouvés dans les couches de roche sédimentaire. Cela donne une indication de ce que la vie était présente sur Terre pendant chaque période géologique.

Différence entre la croissance exponentielle et la décroissance exponentielle

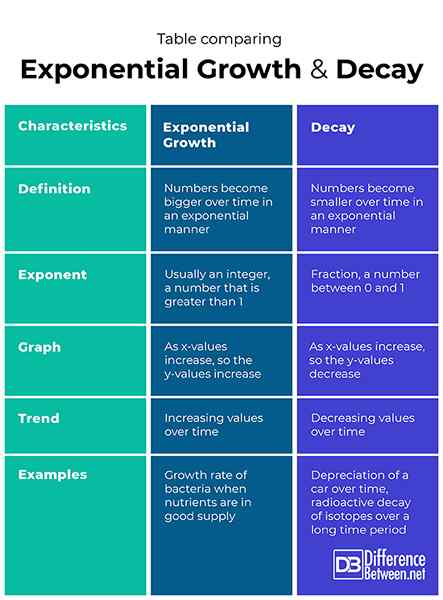
Définition

Dans la croissance exponentielle, les nombres augmentent de valeur au fil du temps de manière exponentielle. En décomposition, les nombres diminuent dans la valeur au fil du temps de manière exponentielle.

Exposant

L'exposant dans l'équation dans le cas de la croissance exponentielle est généralement un entier, un nombre supérieur à 1. L'exposant de l'équation de la décroissance est une fraction comprise entre 0 et 1.

Graphique

Dans le cas d'une croissance exponentielle, les valeurs Y d'un graphique augmenteront à mesure que les valeurs X augmenteront. Dans la situation de la décomposition, les valeurs y sur le graphique diminueront à mesure que les valeurs X augmenteront.

S'orienter

La tendance qui est évidente dans la croissance exponentielle est de plus en plus importante au fil du temps. La tendance de la décroissance est l'inverse de celle observée avec une croissance exponentielle et à la place, il est de plus en plus petit au fil du temps.

Exemples

Les exemples de taux de croissance exponentiel incluent les taux de croissance de plusieurs types de bactéries lorsque les conditions sont optimales et avant que le substrat ne soit épuisé. Les exemples de désintégration incluent la valeur décroissante d'une voiture (dépréciation) au fil du temps et la désintégration radioactive des isotopes radioactifs avec le temps.

Tableau comparant la croissance exponentielle et la décomposition

Résumé de la croissance exponentielle vs. Carie

• La croissance exponentielle et la désintégration peuvent être décrites mathématiquement en utilisant des équations impliquant un exposant.
• La croissance exponentielle et la désintégration impliquent un changement rapide des nombres.
• L'exposant de la croissance exponentielle est toujours positif et supérieur à 1.
• L'exposant de la décroissance est toujours comprise entre 0 et 1.
• La croissance exponentielle est lorsque les nombres augmentent rapidement de manière exponentielle, donc pour chaque valeur X sur un graphique, il y a une plus grande valeur Y.
• La désintégration est lorsque les nombres diminuent rapidement de manière exponentielle, donc pour chaque valeur X sur un graphique, il y a une valeur y plus petite.
• Un exemple de croissance exponentielle est le taux de croissance démographique rapide des bactéries.
• Un exemple de désintégration est l'amortissement de la valeur d'une voiture et la désintégration radioactive des isotopes.