Différence entre FFT et DFT

Transformée de Fourier rapide (FFT) vs. Transformée de Fourier discrète (DFT)

La technologie et la science vont de pair. Et il n'y a pas de meilleur exemple de cela que le traitement numérique du signal (DSP). Le traitement du signal numérique est le processus d'optimisation de la précision et de l'efficacité des communications numériques. Tout est des données - que ce soit les images des sondes spatiales externes ou des vibrations sismiques et tout ce qui est entre les deux. Pour convertir ces données en format lisible par l'homme à l'aide d'ordinateurs, c'est le traitement du signal numérique. C'est l'une des technologies les plus puissantes qui combine à la fois la théorie mathématique et la mise en œuvre physique. L'étude du DSP a commencé comme un cours de niveau supérieur en génie électrique, mais au fil du temps, il est devenu un Gamechanger potentiel dans le domaine de la science et de l'ingénierie. Il suffit de dire que sans DSP, les ingénieurs et les scientifiques pourraient cesser d'exister.

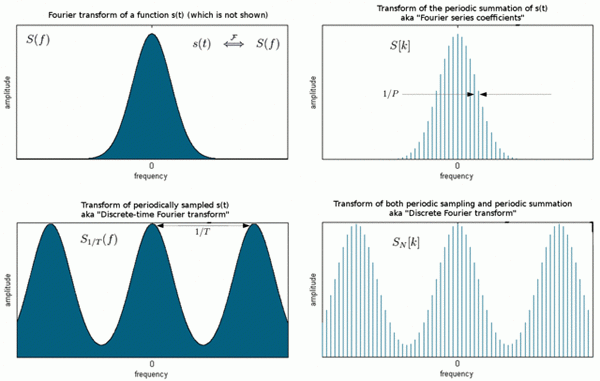
La transformée de Fourier est un moyen de cartographier un signal, dans le domaine de temps ou d'espace dans son spectre dans le domaine fréquentiel. Les domaines de temps et de fréquence ne sont que des moyens alternatifs de représentation des signaux et la transformée de Fourier est la relation mathématique entre les deux représentations. Un changement de signal dans un domaine affecterait également le signal dans l'autre domaine, mais pas nécessairement de la même manière. La transformée de Fourier discrète (DFT) est une transformation comme une transformée de Fourier utilisée avec des signaux numérisés. Comme son nom l'indique, c'est la version discrète du FT qui considère à la fois le domaine temporel et le domaine fréquentiel comme périodique. Fast Fourier Transform (FFT) n'est qu'un algorithme pour un calcul rapide et efficace du DFT.

Transformée de Fourier discrète (DFT)

La transformation discrète de Fourier (DFT) est l'un des outils les plus importants du traitement du signal numérique qui calcule le spectre d'un signal de durée finie. Il est très courant de coder les informations dans les sinusoïdes qui forment un signal. Cependant, dans certaines applications, la forme d'une forme d'onde de domaine temporel n'est pas une application pour les signaux, auquel le contenu de fréquence du signal devient très utile d'une manière autre que les signaux numériques. La représentation d'un signal numérique en termes de composante de fréquence dans un domaine de fréquence est importante. L'algorithme qui transforme les signaux du domaine temporel en composants de domaine de fréquence est connu sous le nom de transformée de Fourier discrète, ou DFT.

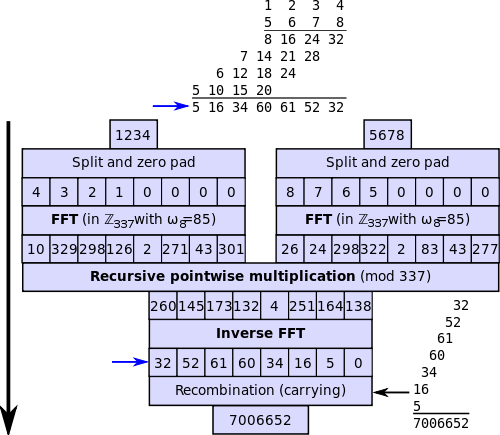
Transformée de Fourier rapide (FFT)

Le Fast Fourier Transform (FFT) est une implémentation du DFT qui produit presque les mêmes résultats que le DFT, mais il est incroyablement plus efficace et beaucoup plus rapide, ce qui réduit souvent le temps de calcul considérablement. C'est juste un algorithme de calcul utilisé pour un calcul rapide et efficace du DFT. Diverses techniques de calcul DFT rapides connues collectivement sous le nom de Transform Furrier rapide, ou FFT. Gauss a été le premier à proposer la technique de calcul des coefficients dans un trigonométrique d'une orbite d'un astéroïde en 1805. Cependant, ce n'est qu'en 1965 qu'un journal fondateur de Cooley et Tukey a attiré l'attention de la communauté des sciences et de l'ingénierie, qui a également jeté les bases de la discipline du traitement du signal numérique.

Différence entre FFT et DFT

1. Signification de FFT et DFT

La transformation discrète de Fourier, ou simplement appelée DFT, est l'algorithme qui transforme les signaux du domaine temporel en composants du domaine fréquentiel. DFT, comme son nom l'indique, est vraiment discret; Les ensembles de données de domaine temporel discrets sont transformés en représentation de fréquence discrète. En termes simples, il établit une relation entre la représentation du domaine temporel et la représentation du domaine fréquentiel. La transformée de Fourier rapide, ou FFT, est un algorithme de calcul qui réduit le temps de calcul et la complexité des grandes transformations. FFT n'est qu'un algorithme utilisé pour le calcul rapide du DFT.

2. Algorithme de FFT et DFT

L'algorithme FFT le plus couramment utilisé est l'algorithme Cooley-Tukey, qui a été nommé d'après J. W. Cooley et John Tukey. C'est un algorithme de division et de conquête pour le calcul de la machine des séries de Fourier complexes. Il brise le DFT en DFT plus petits. D'autres algorithmes FFT incluent l'algorithme du Rader, l'algorithme de transformation de Fourier Winograd, l'algorithme de transformation Z Chirp, etc. Les algorithmes DFT peuvent être programmés sur des ordinateurs numériques à usage général ou implémentés directement par matériel spécial. L'algorithme FFT est utilisé pour calculer le DFT d'une séquence ou son inverse. Un dft peut être effectué comme o (n²) Dans la complexité du temps, tandis que FFT réduit la complexité temporelle dans l'ordre de O (nlogn).

3. Applications de FFT et DFT

La DFT peut être utilisée dans de nombreux systèmes de traitement numérique dans une variété d'applications telles que le calcul du spectre de fréquence d'un signal, la résolution d'applications différentielles partielles, la détection des cibles à partir d'échos radar, l'analyse de corrélation, le calcul de la multiplication polynomiale, l'analyse spectrale, et plus encore. La FFT a été largement utilisée pour les mesures acoustiques dans les églises et les salles de concert. D'autres applications de FFT incluent l'analyse spectrale dans les mesures vidéo analogiques, les grands entiers et la multiplication polynomiale, le filtrage des algorithmes, le calcul des distributions isotopiques, le calcul des coefficients de la série Fourier, le calcul des convolutions, la génération de bruit à faible fréquence, la conception de kinoformes, l'exécution de matrices structurées dense, le traitement d'image et plus.

FFT VS. DFT: Graphique de comparaison

Résumé de FFT vs. Dft

En un mot, la transformée de Fourier discrète joue un rôle clé dans la physique car il peut être utilisé comme outil mathématique pour décrire la relation entre le domaine temporel et la représentation du domaine fréquentiel des signaux discrets. C'est un algorithme simple mais assez long. Cependant, pour réduire le temps de calcul et la complexité des grandes transformations, un algorithme plus complexe mais moins chronophage tel que la transformation rapide de Fourier peut être utilisé. FFT est une implémentation du DFT utilisé pour le calcul rapide du DFT. En bref, FFT peut faire tout ce qu'un DFT fait, mais plus efficacement et beaucoup plus rapide qu'un DFT. C'est un moyen efficace de calculer le DFT.