Différence entre le demi-additionneur et l'additionneur complet
- 1968
- 212
- Anaïs Fournier
L'additionneur complet et le demi-additionneur sont les éléments de circuit numérique utilisés pour résumer les nombres. Dans les ordinateurs modernes, ils font partie de l'unité logique arithmétique qui est responsable de la réalisation d'opérations arithmétiques. Adder travaillent avec des signaux électriques représentant le nombre binaire d'ordinateurs. En électronique, l'additionneur est un circuit numérique qui ajoute des nombres. Dans de nombreux ordinateurs et autres processeurs, les aders sont non seulement utilisés dans l'unité arithmétique-logique, mais aussi dans d'autres parties où il est nécessaire de calculer l'adresse, les tables d'index et les opérations similaires. Bien que les ajouts puissent être construits pour diverses représentations de nombres, telles que les nombres décimaux codés binaires, ils sont généralement des amers à numéro binaire.

Qu'est-ce que Half Adder?
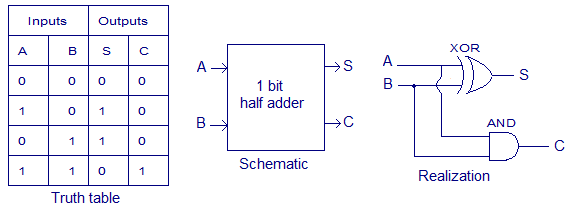
Le demi-additionneur ajoute deux bits ensemble. Le demi-additionneur a deux signaux d'entrée représentant des chiffres binaires (A et B) et deux signaux de sortie, dont l'un est le résultat du ou des ajout (s), et le second le transport en classe supérieure (C). Il est important de noter qu'un demi-additionneur ne peut pas être utilisé pour ajouter des nombres binaires à plusieurs chiffres car il n'y a pas de transport de niveau inférieur. Le demi-additionneur est un circuit combiné de XOR et et des circuits. Son objectif, comme son nom l'indique, est d'ajouter des nombres. Le processus d'ajout de nombres dans le système binaire est réduit à l'ajout de chiffres, où en conséquence nous obtenons une somme et un transport. Étant donné que le demi-additionneur lui-même ne peut pas calculer le résultat entier, il est combiné avec un autre demi-additionneur et ou un circuit pour faire un additionneur complet.
La table de vérité utilisée pour décrire le travail d'un demi-additionneur est:
| un | b | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
où s = a⊕b; C = a * b
Qu'est-ce que l'additionneur?
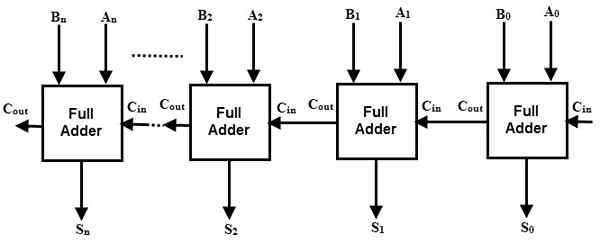
Afin d'ajouter des nombres dans un système binaire, nous devons collecter 3 chiffres en ajoutant un portage précédent à la somme de deux chiffres. Ceci est accompli en utilisant deux demi-adels et ou des circuits. La différence entre le demi-additionneur et l'addition. L'additionneur complet a: trois signaux d'entrée, dont deux représentent les chiffres binaires (A et B), et une troisième entrée étant le portage de la classe précédente (CIN); Deux signaux de sortie, dont l'un est le résultat du ou des ajout (s), et le deuxième transport dans la classe supérieure (COUT). Puisqu'un additionneur complet a le portage précédent comme signal d'entrée, il peut être utilisé pour ajouter des nombres binaires à plusieurs chiffres. Les nombres binaires à plusieurs chiffres sont ajoutés par une connexion en cascade de plusieurs ajouts complets. Le nombre d'ajouteurs complets dans la connexion en cascade est égal au nombre de chiffres, c'est-à-dire les bits qui ont des nombres à ajouter (un additionneur pour chaque bit).
La table de vérité utilisée pour décrire le travail d'un additionneur complet est:
| un | b | Cin | S | Coup de coude |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
où s = a⊕b⊕cin; Cout = (a * b) + (cin * (a⊕b))
Différence entre le demi-additionneur et l'additionneur complet
-
Définition de la moitié et de l'additionneur complet
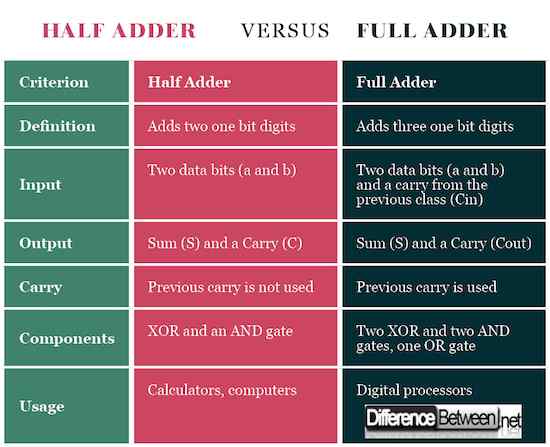
Le demi-additionneur et l'additionneur complet sont des circuits combinaison. Cependant, le premier ajoute deux chiffres d'un bit, tandis que le second ajoute trois chiffres.
-
Entrée de la moitié et de l'additionneur complet
Le demi-additionneur a deux valeurs d'entrée - A et B qui représentent les bits de données. L'additionneur complet a une entrée supplémentaire - le transport de la classe inférieure (CIN).
-
Sortie de la moitié et de l'additionneur complet
Le demi-additionneur a deux sorties. L'un est la somme du (s) processus (s) et l'autre est le transport de la sommation (c). L'additionneur complet a également deux sorties (s; cout).
-
Porter
En cas de demi-additionneur, le transport de la classe inférieure (itération précédente) n'est pas ajouté dans la nouvelle classe. En cas d'additionneur complet, le portage est transféré dans la nouvelle classe, ce qui permet à l'addition.
-
Composants de la moitié et de l'additionneur complet
Le demi-additionneur est constitué de XOR et An et Gate. L'additionneur complet est principalement deux demi-ajouts combinés ensemble - se compose de deux XOR et deux et des portes et une ou porte.
-
Utilisation de la moitié et de l'additionneur complet
Les demi-ajouts sont utilisés dans les ordinateurs, les calculatrices, les appareils de mesure, etc. Les additionnes complètes sont utilisées dans le traitement numérique.
Half Adder vs. Adder complet: table de comparaison
Résumé des demi-versets Adder complet
- Lorsque deux nombres binaires sont ajoutés, d'abord les chiffres sont ajoutés, je.e. les plus petits morceaux. Cette opération est effectuée par un demi-additionneur en tant que réseau le plus simple qui permet de résumer deux nombres à un bits. Les signaux d'entrée du réseau sont les chiffres binaires des chiffres, et les sorties résultantes sont la somme et le transport.
- Lorsque des numéros à plusieurs chiffres sont ajoutés, le réseau de demi-additionneur ne peut être utilisé que pour assembler les plus petits chiffres, car le demi-additionneur ne peut pas résumer le chiffre de transport de la classe précédente. La base de tous les appareils arithmétiques numériques est le soi-disant additionneur complet. Ce réseau est utilisé pour ajouter trois numéros à un chiffre. Deux nombres sont attribués, et le troisième est le transport des calculs de classe précédents.
- « Différence entre le scrutin et l'interruption
- Différence entre l'hypoglycémie et l'hyperglycémie »

