Différence entre asymptote horizontal et vertical

Avant d'entrer dans le sujet de l'asymptote horizontale et verticale, essayons de comprendre ce que sont exactement les asymptotes et quel rôle ils jouent en mathématiques. En géométrie projective, une asymptote est une ligne droite qui aborde arbitrairement une courbe donnée mais ne se rencontre à aucune distance finie. Géométriquement, une ligne est une asymptote d'une courbe y = f (x), si la distance entre la ligne et un point «p» sur la courbe s'approche de zéro comme x et y ont tous deux tendance à infinier. Un graphique peut avoir une asymptote parallèle à chaque axe. En fait, une asymptote est quelque chose qui n'est pas là physiquement - cela ressemble plus.

Une asymptote aide à déterminer les actions ou les formes des choses, mais ce n'est pas vraiment une partie du graphique. C'est simplement une ligne imaginaire qui vous aide à graphiquement une fonction rationnelle. Alors que la courbe s'approche d'une asymptote, elle se rapproche de plus en plus de l'asymptote mais ne la touche jamais réellement. Ainsi, l'asymptote aide à déterminer où le graphique de la fonction peut ou ne peut pas aller. Cela étant dit, il existe trois types d'asymptotes: les asymptotes verticaux, horizontaux et obliques. Mais nous ne discuterons que des asymptotes verticaux et des asymptotes horizontaux, et voir comment comprendre lequel est ce qui est réellement.

Qu'est-ce que l'asymptote horizontale?

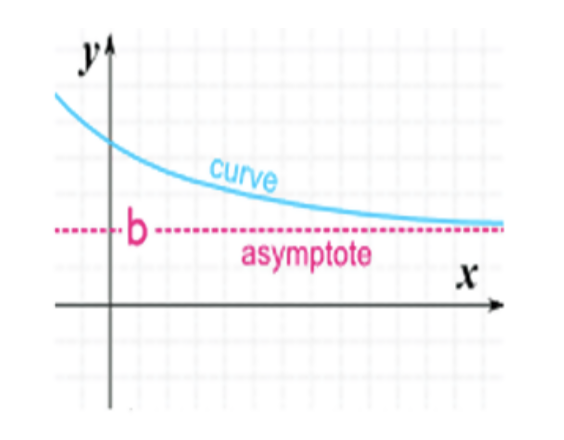
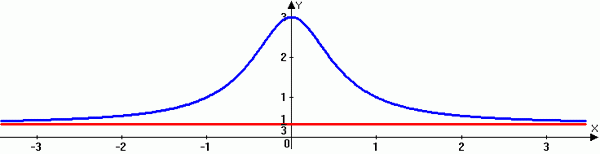
Une asymptote horizontale est une valeur constante sur un graphique qu'une fonction approche mais n'atteint pas réellement. Il indique ce qui arrive réellement à la courbe à mesure que les valeurs X deviennent très grandes ou très petites. Dans les exemples graphiques ci-dessus, la courbe s'approche d'une valeur constante B, mais n'atteint jamais réellement, y = 0.

La ligne y = b est une asymptote horizontale du graphique de 'f' si f (x) -> b comme x -> ∞ ou x -> - ∞

Pour trouver une asymptote horizontale d'une fonction rationnelle, le degré des polynômes dans le numérateur et le dénominateur doit être considéré.

• Si le dénominateur a la puissance variable la plus élevée dans l'équation de la fonction, l'asymptote horizontal est automatiquement l'axe x ou y = 0.
• Si le numérateur et le dénominateur ont un degré égal, prenez les coefficients principaux de ces termes avec la plus grande puissance et faites-en une fraction pour trouver l'asymptote horizontal
• Si le numérateur a la puissance variable la plus élevée dans l'équation de la fonction, la fonction n'a pas d'asymptote horizontale; Le graphique aura probablement une asymptote oblique.

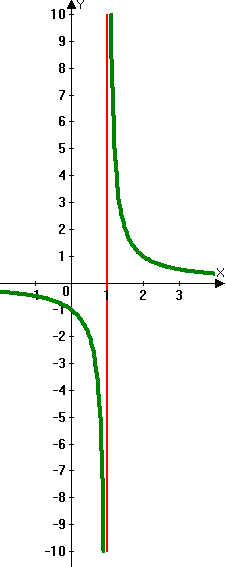
Qu'est-ce que l'asymptote verticale?

Comme le dénominateur d'une fraction ne peut jamais être nul, avoir la variable en bas si une fraction peut être un problème. Une certaine valeur de domaine de «x» rend le dénominateur zéro et la fonction sautera par-dessus cette valeur dans le graphique, créant une asymptote verticale. Ce sont des lignes verticales dessinées à la légère ou avec des tirets pour montrer qu'ils ne font pas partie du graphique.

Si le nombre réel «a» est un zéro du dénominateur Q (x), alors le graphique de f (x) = p (x) / q (x), où p (x) et q (x) n'ont pas de commun facteurs, a l'asymptote verticale, x = a.

Différence entre asymptote horizontal et vertical

Définition

- Une asymptote horizontale est une valeur constante sur un graphique qu'une fonction approche mais n'atteint pas réellement. Il indique ce qui arrive réellement à la courbe à mesure que les valeurs X deviennent très grandes ou très petites. Les asymptotes verticaux, en revanche, sont des lignes verticales invisibles qui correspondent au zéro dans le dénominateur d'une fraction rationnelle. Ce sont des lignes verticales dessinées à la légère ou avec des tirets pour montrer qu'ils ne font pas partie du graphique.

Calcul

- Pour déterminer une asymptote horizontale d'une fonction rationnelle, le degré des polynômes dans le numérateur et le dénominateur doit être considéré. Si le dénominateur a la puissance variable la plus élevée dans l'équation de la fonction, l'asymptote horizontal est automatiquement l'axe x ou y = 0. Si le numérateur et le dénominateur ont un degré égal, faites une fraction de leurs coefficients pour déterminer l'équation horizontale asymptote. Pour déterminer les asymptotes verticales d'une fonction rationnelle, définissez le dénominateur de la fraction égale à zéro.

Exemple

- Découvrons les asymptotes de la fonction

Y = 3x²+9x-21 ∕ x²-25

Pour trouver les asymptotes verticaux, définissez le dénominateur de la fraction égale à zéro.

X²-25 = 0

(x-5) (x + 5) = 0

x = 5 et x = - 5

Ces deux nombres sont les deux valeurs qui ne peuvent pas être incluses dans le domaine, donc les équations sont des asymptotes verticaux. Ainsi, les deux asymptotes verticaux sont, x = 5 et x = - 5.

Maintenant, pour déterminer l'asymptote horizontale, regardez l'équation d'origine. Ici, la puissance variable la plus élevée est 2. Comme le numérateur et le dénominateur ont le même degré de puissance, font une fraction de leurs coefficients:

y = 3x²/X²

y = 3/1

y = 3

Ainsi, l'équation de l'asymptote horizontale est, y = 3.

Asymptote horizontale vs. Asymptote verticale: tableau de comparaison

Résumé de l'asymptote horizontale vs. Asymptote vertical

Une asymptote aide à déterminer les actions ou les formes des choses, mais ce n'est pas vraiment une partie du graphique. Les asymptotes verticaux marquent les endroits où la fonction n'a pas de domaine. Vous résolvez pour l'équation des asymptotes verticales en définissant le dénominateur de la fraction égale à zéro. Les asymptotes horizontaux, en revanche, indiquent ce qui arrive à la courbe à mesure que les valeurs X deviennent très grandes ou très petites. Pour trouver une asymptote horizontale, vous devez considérer le degré des polynômes dans le numérateur et le dénominateur.