Différence entre les événements mutuellement exclusifs et indépendants
- 5104
- 1289
- Mathilde Roux
 La probabilité est un concept mathématique, qui est maintenant devenu une discipline à part entière et est une partie vitale des statistiques. L'expérience aléatoire dans la probabilité est une performance qui génère un certain résultat, purement basé sur le hasard. Les résultats d'une expérience aléatoire sont appelés événements. En probabilité, il existe différents types d'événements, comme dans simple, composé, mutuellement exclusif, exhaustif, indépendant, dépendant, tout aussi probable, etc. Lorsque les événements ne peuvent pas se produire en même temps, ils sont appelés mutuellement exclusif
La probabilité est un concept mathématique, qui est maintenant devenu une discipline à part entière et est une partie vitale des statistiques. L'expérience aléatoire dans la probabilité est une performance qui génère un certain résultat, purement basé sur le hasard. Les résultats d'une expérience aléatoire sont appelés événements. En probabilité, il existe différents types d'événements, comme dans simple, composé, mutuellement exclusif, exhaustif, indépendant, dépendant, tout aussi probable, etc. Lorsque les événements ne peuvent pas se produire en même temps, ils sont appelés mutuellement exclusif
D'un autre côté, si chaque événement n'est pas affecté par d'autres événements, ils sont appelés événements indépendants. Prenez une lecture complète de l'article présenté ci-dessous pour mieux comprendre la différence entre les événements mutuellement exclusifs et indépendants.
Contenu: événement mutuellement exclusif vs événement indépendant
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Des événements mutuellement exclusifs | Événements indépendants |
|---|---|---|
| Signification | Deux événements seraient mutuellement exclusifs, lorsque leur occurrence n'est pas simultanée. | Deux événements seraient indépendants, lorsque la survenue d'un événement ne peut contrôler l'occurrence. |
| Influence | La présence d'un événement entraînera la non-occurrence de l'autre. | L'occurrence d'un événement n'aura aucune influence sur la survenue de l'autre. |
| Formule mathématique | P (a et b) = 0 | P (a et b) = p (a) p (b) |
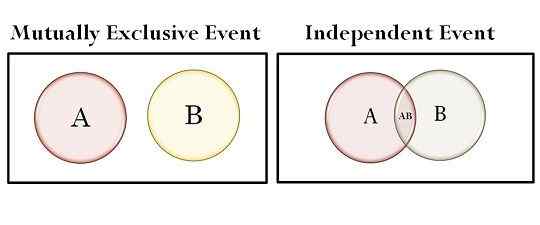
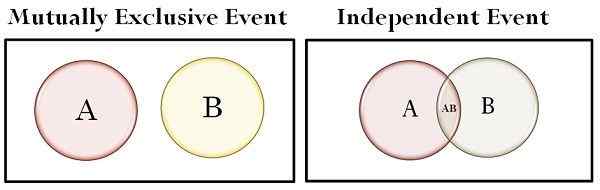
| Sets dans le diagramme de Venn | Ne chevauche pas | Chevauchement |
Définition de l'événement mutuellement exclusif
Les événements mutuellement exclusifs sont ceux qui ne peuvent pas se produire simultanément, je.e. où l'occurrence d'un événement se traduit par la non-occurrence de l'autre événement. De tels événements ne peuvent pas être vrais en même temps. Par conséquent, l'événement d'un événement rend impossible l'événement d'un autre événement. Ceux-ci sont également connus sous le nom d'événements disjoints.
Prenons un exemple de lancement d'une pièce, où le résultat serait soit la tête ou la queue. La tête et la queue ne peuvent pas se produire simultanément. Prenez un autre exemple, supposons que si une entreprise souhaite acheter des machines, pour lesquelles elle a deux options de machine A et B. La machine qui est rentable et la productivité est meilleure, sera sélectionnée. L'acceptation de la machine A entraînera automatiquement le rejet de la machine B et vice versa.
Définition de l'événement indépendant
Comme son nom l'indique, les événements indépendants sont les événements, dans lesquels la probabilité d'un événement ne contrôle pas la probabilité de l'occurrence de l'autre événement. L'évaluation ou le non-happement d'un tel événement n'a absolument aucun effet sur la survenue ou le non-effusion d'un autre événement. Le produit de leurs probabilités distinctes est égale à la probabilité que les deux événements se produisent.
Prenons un exemple, supposons que si une pièce est lancée deux fois, la queue dans la première chance et la queue dans la seconde, les événements sont indépendants. Un autre exemple à cela, supposons que si un dés est roulé deux fois, 5 dans la première chance et 2 dans le second, les événements sont indépendants.
Différence clé entre les événements mutuellement exclusifs et indépendants
Les différences significatives entre les événements mutuellement exclusifs et indépendants sont élaborés comme sous:
- Les événements mutuellement exclusifs sont les événements où leur occurrence n'est pas simultanée. Lorsque l'occurrence d'un événement ne peut contrôler la survenue d'autres, ces événements sont appelés événements indépendants.
- Dans les événements mutuellement exclusifs, la survenue d'un événement entraînera la non-occurrence de l'autre. Inversement, dans les événements indépendants, l'occurrence d'un événement n'aura aucune influence sur la survenue de l'autre.
- Les événements mutuellement exclusifs sont représentés mathématiquement comme P (A et B) = 0 tandis que les événements indépendants sont représentés comme P (A et B) = P (A) P (B).
- Dans un diagramme de Venn, les ensembles ne se chevauchent pas, dans le cas d'événements mutuellement exclusifs tandis que si nous parlons d'événements indépendants, les ensembles chevauchent.
Conclusion
Donc, avec la discussion ci-dessus, il est clair que les deux événements ne sont pas les mêmes. De plus, il y a un point à retenir, et c'est si un événement s'exclut mutuellement, alors il ne peut pas être indépendant et vice versa. Si deux événements A et B s'excluent mutuellement, ils peuvent être exprimés en P (Aub) = P (a) + P (b) tandis que si les mêmes variables sont indépendantes, ils peuvent être exprimés en P (a∩b) = P (a) p (b).
- « Différence entre la personnalité de type A et de type B
- Différence entre la rémunération et les avantages »

