Différence entre la parabole et l'hyperbole

Parabole vs hyperbola

La parabole et l'hyperbole sont deux sections différentes d'un cône. Nous pouvons gérer leurs différences dans une explication mathématique ou gérer les différences de manière très simple que non seulement les mathématiciens mais tout le monde peuvent comprendre. Cet article essaiera d'expliquer la différence entre eux d'une manière très simple.
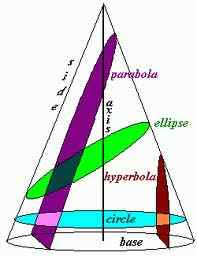
Tout d'abord, lorsqu'une figure solide, qui dans ce cas est un cône, est coupée par un plan, la section qui est obtenue est appelée une section conique. Les sections coniques peuvent être des cercles, des ellipses, des hyperbolas et des parabolas en fonction de l'angle d'intersection entre l'axe du cône et le plan. Les parabolas et les hyperbolas sont une courbe ouverte, ce qui signifie que les bras ou les branches des courbes continuent à l'infini; Ce ne sont pas des courbes fermées comme un cercle ou une ellipse.

Parabole
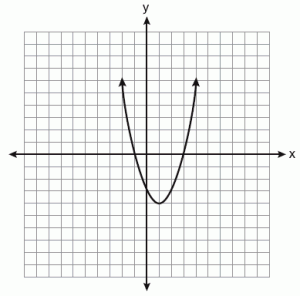
Une parabole est la courbe obtenue lorsque le plan coupe parallèle au côté cône. Dans une parabole, une ligne passant par la focalisation et perpendiculaire à la directrice est appelée «axe de symétrie.«Lorsque la parabole est croisée par le point sur« l'axe de symétrie », il est appelé« sommet.«Tous les parabolas sont façonnés de manière identique car ils sont coupés à un angle spécifique. C'est un caractérisé par l'excentricité de «1."C'est la raison pour laquelle ils sont tous de la même forme mais peuvent être de tailles différentes.

La parabole est donnée par l'équation y2 = x
Lorsqu'un ensemble de points présents dans un plan est équidistant de la directrice, une ligne droite donnée, et sont équidistants de la focalisation, un point donné qui est fixé, il est appelé parabole.
Les parabolas ont de nombreuses applications pratiques. Ils sont utilisés pour concevoir le chemin des missiles, des réflecteurs de phares des automobiles, des télescopes, des récepteurs radar et des plats de satellite.

Hyperbole

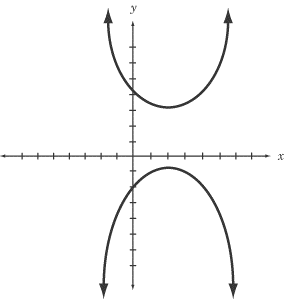
L'hyperbole est la courbe obtenue lorsque le plan coupe presque parallèle à l'axe. Les hyperbolas ne sont pas de forme identique car il existe de nombreux angles entre l'axe et le plan. Les «sommets» sont les points sur les deux bras les plus proches; tandis que le segment de ligne qui relie les bras est appelé «axe majeur."
Dans une parabole, les deux bras de la courbe, également appelés branches, deviennent parallèles les uns aux autres. Dans une hyperbole, les deux bras ou courbes ne deviennent pas parallèles. Un centre d'hyperbola est le milieu de l'axe majeur.

L'hyperbole est donnée par l'équation xy = 1

Lorsque la différence de distances entre un ensemble de points présents dans un plan vers deux foyers fixes ou points est une constante positive, elle est appelée hyperbole.

Résumé:
Lorsqu'un ensemble de points présents dans un plan est équidistant de la directrice, une ligne droite donnée, et sont équidistants de la focalisation, un point donné qui est fixé, il est appelé parabole. Lorsque la différence de distances entre un ensemble de points présents dans un plan vers deux foyers fixes ou points est une constante positive, elle est appelée hyperbole.
Tous les parabolas sont de la même forme quelle que soit la taille; Toutes les hyperbolas sont de différentes formes
La parabole est donnée par l'équation y2 = x; Une hyperbole est donnée par l'équation xy = 1
Dans une parabole, les deux bras deviennent parallèles les uns aux autres alors que dans une hyperbole, ils ne.