Différence entre la permutation et la combinaison

- 4510
- 87
- Mathilde Roux
 En mathématiques, vous avez peut-être entendu les notions de permutation et de fin du nombre de fois, mais avez-vous déjà imaginé que ces deux sont des concepts différents? La différence fondamentale entre la permutation et la combinaison est l'ordre des objets, dans permutation L'ordre des objets est très important, je.e. L'arrangement doit être dans l'ordre stipulé du nombre d'objets, pris uniquement ou tous à la fois.
En mathématiques, vous avez peut-être entendu les notions de permutation et de fin du nombre de fois, mais avez-vous déjà imaginé que ces deux sont des concepts différents? La différence fondamentale entre la permutation et la combinaison est l'ordre des objets, dans permutation L'ordre des objets est très important, je.e. L'arrangement doit être dans l'ordre stipulé du nombre d'objets, pris uniquement ou tous à la fois.
Contre cela, dans le cas d'un combinaison, La commande n'a pas du tout. Non seulement en mathématiques, mais aussi dans la vie pratique, nous passons régulièrement avec ces deux concepts. Bien que nous ne le remarquons jamais. Alors, lisez attentivement l'article pour savoir comment ces deux concepts sont différents.
Contenu: combinaison Permutation vs
- Tableau de comparaison
- Définition
- Différences clés
- Exemple
- Conclusion
Tableau de comparaison
| Base de comparaison | Permutation | Combinaison |
|---|---|---|
| Signification | La permutation fait référence aux différentes façons d'organiser un ensemble d'objets dans un ordre séquentiel. | La combinaison fait référence à plusieurs façons de choisir des éléments d'un large ensemble d'objets, de sorte que leur ordre n'a pas d'importance. |
| Commande | Pertinent | Non pertinent |
| Indique | Arrangement | Sélection |
| Qu'est-ce que c'est? | Éléments ordonnés | Ensembles non ordonnés |
| Réponses | Combien d'arrangements différents peut être créé à partir d'un ensemble d'objets donnés? | Combien de groupes différents peuvent être choisis parmi un plus grand groupe d'objets? |
| Dérivation | Permutation multiple à partir d'une seule combinaison. | Combinaison unique à partir d'une seule permutation. |
Définition de la permutation
Nous définissons la permutation comme différentes façons d'organiser certains ou tous les membres d'un ensemble dans un ordre spécifique. Cela implique tous les dispositions ou réarrangements possibles de l'ensemble donné, dans l'ordre distincable.
Par exemple, Toute permutation possible créée avec les lettres x, y, z -
- En prenant les trois à la fois, XYZ, XZY, YXZ, YZX, ZXY, ZYX.
- En prenant deux à la fois sont XY, XZ, YX, YZ, ZX, ZY.
Le nombre total de permutations possibles de n choses, prises r à la fois, peut être calculée comme suit:
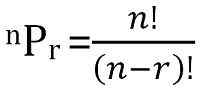
Définition de la combinaison
La combinaison est définie comme les différentes manières, de sélectionner un groupe, en prenant certains ou tous les membres d'un ensemble, sans l'ordre suivant.
Par exemple, Toutes les combinaisons possibles choisies avec la lettre m, n, o -
- Lorsque trois lettres sur trois doivent être sélectionnées, alors la seule combinaison est MNO
- Lorsque deux lettres sur trois doivent être sélectionnées, les combinaisons possibles sont MN, non, OM.
Le nombre total de combinaisons possibles de n choses, prises r à la fois, peut être calculée comme suit:
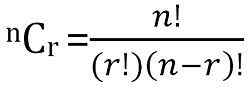
Différences clés entre la permutation et la combinaison
Les différences entre la permutation et la combinaison sont clairement établies sur les motifs suivants:
- Le terme permutation fait référence à plusieurs façons d'organiser un ensemble d'objets dans un ordre séquentiel. La combinaison implique plusieurs façons de choisir des articles à partir d'un grand pool d'objets, de sorte que leur commande n'est pas pertinente.
- Le principal point de distinction entre ces deux concepts mathématiques est l'ordre, le placement et la position, je.e. Dans les caractéristiques de permutation mentionnées ci-dessus, ce qui n'a pas d'importance dans le cas de la combinaison.
- La permutation indique plusieurs façons d'organiser des choses, des gens, des chiffres, des alphabets, des couleurs, etc. D'un autre côté, la combinaison indique différentes façons de sélectionner les éléments de menu, la nourriture, les vêtements, les sujets, etc.
- La permutation n'est rien d'autre qu'une combinaison ordonnée tandis que la combinaison implique des ensembles non ordonnés ou un appariement des valeurs dans des critères spécifiques.
- De nombreuses permutations peuvent être dérivées d'une seule combinaison. Inversement, une seule combinaison peut être obtenue à partir d'une seule permutation.
- La permutation répond combien de dispositions différentes peuvent être créées à partir d'un ensemble donné d'objets? Par opposition à la combinaison qui explique combien de groupes différents peuvent être choisis dans un plus grand groupe d'objets?
Exemple
Supposons qu'il y ait une situation où vous devez trouver le nombre total d'échantillons possibles de deux sur trois objets A, B, C. Dans cette question, tout d'abord, vous devez comprendre si la question est liée à la permutation ou à la combinaison et que la seule façon de le découvrir est de vérifier si l'ordre est important ou non.
Si la commande est importante, la question est liée à la permutation et que les échantillons possibles seront, AB, BA, BC, CB, AC, CA. Où, AB est différent de BA, la Colombie-Britannique est différente de CB et AC est différent CA.
Si l'ordre n'est pas pertinent, la question est liée à la combinaison, et les échantillons possibles seront AB, BC et CA.
Conclusion
Avec la discussion ci-dessus, il est clair que la permutation et la combinaison sont des termes différents, qui sont utilisés en mathématiques, statistiques, recherche et notre vie quotidienne. Un point à retenir, concernant ces deux concepts est que, pour un ensemble donné d'objets, la permutation sera toujours plus élevée que sa combinaison.
- « Différence entre la comptabilité et l'audit
- Différence entre la coentreprise et l'alliance stratégique »

