Différence entre le rapport et la proportion

- 1278
- 169
- Adrien Jean
 Le rapport et la proportion sont deux concepts mathématiques qui ont un nombre final d'applications pratiques dans différentes sphères de la vie. Le rapport est utilisé pour comparer les quantités de deux catégories différentes comme le rapport des hommes aux femmes de la ville. Ici, les hommes et les femmes sont les deux catégories différentes.
Le rapport et la proportion sont deux concepts mathématiques qui ont un nombre final d'applications pratiques dans différentes sphères de la vie. Le rapport est utilisé pour comparer les quantités de deux catégories différentes comme le rapport des hommes aux femmes de la ville. Ici, les hommes et les femmes sont les deux catégories différentes.
Au contraire, Proportion est utilisé pour découvrir la quantité d'une catégorie sur le total, comme la proportion d'hommes à partir de personnes totales vivant dans la ville.
Le rapport définit la relation quantitative entre deux quantités, représentant le nombre de temps, une valeur contient l'autre. Inversement, la proportion est cette partie qui explique la relation comparative avec toute la partie. Cet article vous présente les différences de base entre le rapport et la proportion. Regarde.
Contenu: ratio vs proportion
- Tableau de comparaison
- Définition
- Différences clés
- Exemple
- Conclusion
Tableau de comparaison
| Base de comparaison | Rapport | Proportion |
|---|---|---|
| Signification | Le rapport fait référence à la comparaison de deux valeurs de la même unité. | Lorsque deux ratios sont définis égaux l'un à l'autre, il est appelé comme proportion. |
| Qu'est-ce que c'est? | Expression | Équation |
| Indiqué par | Colon (:) signe | Double côlon (: :) ou égal à (=) signe |
| Représente | Relation quantitative entre deux catégories. | Relation quantitative d'une catégorie et du total |
| Mot-clé | 'À chaque' | 'Hors de' |
Définition du rapport
En mathématiques, le rapport est décrit comme la comparaison de la taille de deux quantités de la même unité, qui est exprimée en termes de temps I.e. Le nombre de fois la première valeur contient la seconde. Il s'exprime sous sa forme la plus simple. Les deux quantités en comparaison sont appelées le Conditions de rapport, où le premier terme est antécédent Et le deuxième terme est conséquent.
Par exemple: 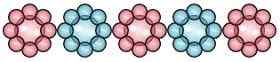 Dans la figure donnée, il y a 3 fleurs rouges à 2 fleurs bleues, je.e. 3: 2. Donc 3 et 2 sont deux quantités de la même unité, la fraction de ces deux quantités (3/2) est connue sous le nom de son rapport. Ici, 3 et 2 sont les termes du rapport, où 3 est antécédent tandis que 2 est conséquente.
Dans la figure donnée, il y a 3 fleurs rouges à 2 fleurs bleues, je.e. 3: 2. Donc 3 et 2 sont deux quantités de la même unité, la fraction de ces deux quantités (3/2) est connue sous le nom de son rapport. Ici, 3 et 2 sont les termes du rapport, où 3 est antécédent tandis que 2 est conséquente.
Il y a peu de points à retenir par rapport au rapport, qui est mentionné comme sous:
- L'anticédent et la conséquence peuvent être multipliés par le même nombre. Le nombre doit être non nul.
- L'ordre des termes est important.
- L'existence du rapport n'est que entre les quantités du même type.
- L'unité des quantités en comparaison devrait également être la même.
- La comparaison de deux ratios ne peut être effectué que s'ils sont équivalents comme la fraction.
Définition de la proportion
La proportion est un concept mathématique, qui indique l'égalité de deux ratios ou fractions. Il se réfère à certaines une catégorie sur le total. Lorsque deux ensembles de nombres, augmentent ou diminuent dans le même rapport, ils seraient directement proportionnels l'un à l'autre.
Par exemple,  1 fleurs sur 3 est rouge = 2 fleurs sur 6 sont rouges.
1 fleurs sur 3 est rouge = 2 fleurs sur 6 sont rouges.
Quatre nombres p, q, r, s sont considérés comme en proportion si p: q = r: s, alors p / q = r / s, i.e. ps = qr (par règle de multiplication croisée). Ici p, q, r, s sont appelés le conditions de proportion, où p est le premier terme, q est le deuxième terme, R est le troisième terme, et S est le quatrième terme. Le premier et le quatrième terme sont appelés extrêmes tandis que le deuxième et le troisième terme sont appelés moyens je.e. moyen terme. De plus, s'il y a trois quantités en proportion continue, la deuxième quantité est la proportion moyenne entre la première et la troisième quantité.
Les propriétés importantes de la proportion sont discutées ci-dessous:
- Invertendo - Si p: q = r: s, alors q: p = s: r
- Alterno - Si P: Q = R: S, alors P: R = Q: S
- Componendo - Si P: Q = R: S, alors P + Q: Q = R + S: S
- Dividendo - Si P: Q = R: S, alors P - Q: Q = R - S: S
- Componendo et Dividendo - Si P: Q = R: S, alors P + Q: P - Q = R + S: R - S
- Addendo - si p: q = r: s, alors p + r: q + s
- Subtrahendo - si p: q = r: s, alors p - r: q - s
Différences clés entre le rapport et la proportion
La différence entre le rapport et la proportion peut être établie clairement pour les motifs suivants:
- Le rapport est défini comme la comparaison des tailles de deux quantités de la même unité. La proportion, en revanche, fait référence à l'égalité de deux ratios.
- Le rapport est une expression tandis que la proportion est une équation qui peut être résolue.
- Le ratio est représenté par le côlon (:) signe entre les quantités comparées. En revanche en revanche, est indiqué par Double Colon (: :) ou égal à (=) signe, entre les ratios en comparaison.
- Le ratio représente la relation quantitative entre deux catégories. Par opposition à la proportion, qui montre la relation quantitative d'une catégorie avec le total.
- Dans un problème donné, vous pouvez identifier s'ils sont en rapport ou en proportion, avec l'aide de mots clés qu'ils utilisent i.e. «à chaque» dans le rapport et «hors» dans le cas de proportion.
Exemple
Il y a au total 80 élèves en classe, dont 30 garçons et le reste des étudiants sont des filles. Découvrez maintenant ce qui suit:
(i) Ratio des garçons aux filles et des filles aux garçons
(ii) Proportion de garçons et de filles dans la classe
Solution: (i) Ratio des garçons aux filles = garçons: filles = 30:50 ou 3: 5
Ratio des filles aux garçons = filles: garçons = 50: 30 ou 5: 3
Ainsi, pour trois garçons, il y a cinq filles ou pour cinq filles, il y a trois garçons.
(ii) Proportion de garçons = 30/80 ou 3/8
Proportion de filles = 50/80 ou 5/8
Ainsi, 3 étudiants sur 8 sont un garçon et 5 étudiants sur 8 sont une fille.
Conclusion
Par conséquent, avec la discussion et les exemples ci-dessus, on peut facilement comprendre les différences entre ces deux concepts mathématiques. Le rapport est la comparaison de deux nombres tandis que la proportion n'est rien d'autre qu'une extension par rapport au rapport qui indique que deux ratios ou fraction sont équivalents.
- « Différence entre le coût du produit et le coût de la période
- Différence entre les actifs et les passifs »

