Différence entre les nombres réels et les entiers

Les mathématiciens ont développé des systèmes pour spécifier en quoi un certain nombre est différent d'un autre. Tout comme les autres concepts, les catégories de nombres se chevauchent. Étant donné que les nombres réels incluent tous les nombres rationnels comme les entiers, ils partagent des caractéristiques similaires telles que l'utilisation de nombres entiers et d'être tracés sur la ligne numérique. Par conséquent, la principale différence est que les nombres réels sont une classification générale tandis que les entiers sont un sous-ensemble qui est caractérisé comme des nombres entiers qui peuvent avoir des propriétés négatives.

Quels sont les nombres réels?

Les nombres réels sont les valeurs que vous pouvez trouver sur la ligne numérique qui est généralement exprimée en tant que ligne horizontale géométrique où un point choisi fonctionne comme «l'origine». Ceux qui tombent sur le côté droit sont étiquetés comme positifs tandis que ceux à gauche sont négatifs. La description «réelle» a été présentée par René Descartes, un célèbre mathématicien et philosophe au XVIIe siècle. Il a particulièrement fait la différence entre les racines réelles des polynômes et leurs racines imaginaires.

Les nombres réels incluent des nombres entiers, entiers, naturels, rationnels et irrationnels:

• Nombres entiers

Les nombres entiers sont des nombres positifs qui n'ont pas de parties fractionnaires ni de décimales car elles représentent des objets entiers sans fragments ni pièces.

• Entiers

Les entiers sont des nombres entiers qui incluent le côté négatif de la ligne numérique.

• Nombres naturels

Également connue sous le nom de nombres de comptage, les nombres naturels sont comme des nombres entiers mais zéro n'est pas inclus car rien ne peut être essentiellement compté comme «0».

• Nombres rationnels

En ce qui concerne ses origines, Pythagore, l'ancien mathématicien grec a proclamé que tous les chiffres étaient rationnels. Les nombres rationnels sont les quotients ou les fractions de deux entiers.  Lorsque P et Q sont à la fois entiers et Q n'est pas équivalent à zéro, P / Q est un nombre rationnel. Par exemple, 3/5 est un nombre rationnel mais 3/0 n'est pas.

• Nombres irrationnels

L'étudiant de Pythagore, Hippasus n'était en désaccord que tous les chiffres étaient rationnels. Grâce à la géométrie, il a prouvé que certains chiffres étaient irrationnels. Par exemple, la racine carrée de deux, qui est 1.41 ne peut pas être exprimé comme une fraction; Par conséquent, c'est irrationnel. Malheureusement, la réalité des nombres rationnels n'a pas été acceptée par les adeptes de Pythagore. Cela a entraîné la noyade d'Hippasus en mer, ce qui serait une punition des dieux pendant cette période.

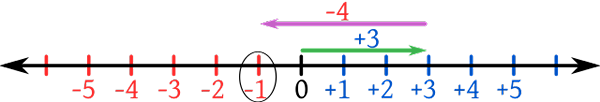
Que sont les entiers?

Du mot latin «entier», qui se traduit par «entier» ou «intact», ces chiffres n'ont pas de composants fractionnaires ou décimaux tout comme les nombres entiers. Les nombres incluent des nombres naturels positifs ou les nombres de comptage et leurs négatifs. Par exemple, -3, -2, -1, 0, -1, 2, 3 sont des entiers. L'illustration habituelle est des nombres également espacés sur une ligne numérique infinie avec zéro, qui n'est ni positif ni négatif, au milieu. Par conséquent, les points positifs sont plus grands que les négatifs.

En ce qui concerne son histoire, les comptes suivants suivent comment les entiers ont été utilisés pour la première fois:

• En 200 b.C. Les nombres négatifs ont d'abord été représentés avec des tiges rouges dans la Chine ancienne.
• Dans environ 630 a.D., Des nombres négatifs ont été utilisés pour représenter la dette en Inde.
• Arbermouth Holst, un mathématicien allemand a introduit des entiers en 1563 comme système en plus et multiplication. Il a développé le système en réponse au nombre croissant de lapins et d'éléphants sur lesquels il expérimentait.

Voici les caractéristiques des entiers:

• Positif

Les nombres du côté droit de la ligne numérique sont positifs et ils représentent souvent la valeur plus élevée de leurs homologues négatifs.

• Négatif

Les nombres du côté gauche de la ligne numérique sont souvent considérés comme la moindre valeur standard de leurs homologues positifs.

• Neutre

Le centre de la ligne numérique, zéro est l'entier qui n'est ni positif ni négatif.

• Pas de fragments

Comme des nombres entiers, les entiers n'ont pas de décimaux ni de fractions.

Différence entre les nombres réels et les entiers

Portée des nombres réels et des entiers

Les nombres réels incluent des nombres entiers, rationnels, irrationnels, naturels et entiers. D'un autre côté, la portée des entiers est principalement préoccupée par des nombres entiers qui sont négatifs et positifs. Par conséquent, les nombres réels sont plus généraux.

Fractions

Les nombres réels peuvent inclure des fractions telles que les nombres rationnels et irrationnels. Cependant, les fractions ne peuvent pas être des entiers.

Propriété la moins élevée

Les nombres réels ont une propriété moins élevée qui est également connue sous le nom de «complétude». Cela signifie qu'un ensemble linéaire de nombres réels a des sous-ensembles avec des qualités de supremum.  Au contraire, les entiers n'ont pas la propriété la moins élevée.

Propriété archimédienne

La propriété archimédienne, qui est l'hypothèse qu'il existe un nombre naturel qui est égal ou supérieur à tout nombre réel, peut être appliqué à des nombres réels. Au contraire, la propriété archimédienne ne peut pas être appliquée aux entiers.

Champ

Les nombres réels sont une sorte de champ qui est une structure algébrique essentielle où les processus arithmétiques sont définis. Au contraire, les entiers ne sont pas considérés comme un champ.

Dénombrable

En jeu, les nombres réels sont innombrables tandis que les entiers sont dénombrables.

Symboles de nombres réels et entiers

Les nombres réels sont symbolisés comme «R» tandis qu'un ensemble d'entiers est symbolisé comme «Z».  N. Bourbaki, un groupe de mathématiciens français dans les années 1930, a spécifié «Z» du mot allemand «Zahlen» qui signifie nombre ou entiers.

Origine des mots pour les nombres réels et les entiers

Les nombres réels ont indiqué les véritables racines d'un polynôme tandis que Integer provenait du mot latin, «entier» car ils n'incluent pas les décimales ni les fractions.

Nombres réels vs entiers

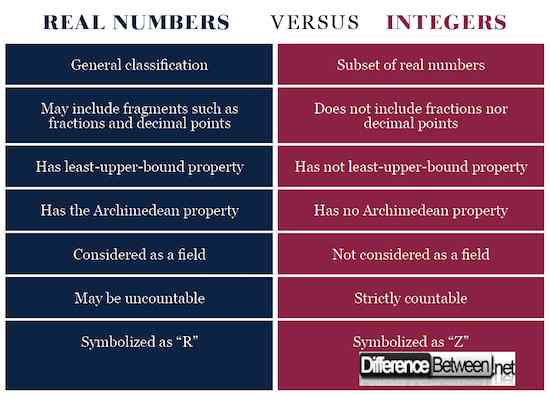
Résumé des nombres réels vs.  Entiers

• Les nombres réels et les entiers peuvent être tracés sur la ligne numérique.
• Les entiers sont un sous-ensemble de nombres réels.
• Les entiers ont des nombres négatifs.
• En tant que ensemble, les nombres réels ont une portée plus générale par rapport aux entiers.
• Contrairement aux entiers, les nombres réels peuvent inclure des fractions et des décimales.
• Les propriétés des champs les moins liés, Archimean et le champ sont généralement applicables aux nombres réels mais pas aux entiers.
• Contrairement aux nombres réels, les entiers sont strictement dénombrables.
• «R» signifie des nombres réels tandis que «z» est pour les entiers.