Différence entre la moyenne de l'échantillon et la moyenne de la population

- 3382
- 3
- Anaïs Fournier
 En statistique, la moyenne arithmétique est l'une des mesures idéales de la tendance centrale. Pour un ensemble donné d'observations, la moyenne arithmétique peut être calculée en ajoutant toutes les observations et en divisant la valeur obtenue par le nombre d'observations. Il y a deux types de moyenne, je.e. Moyenne d'échantillon et moyenne de population, qui est souvent utilisée dans les statistiques et la probabilité. La moyenne de l'échantillon est principalement utilisée pour estimer la moyenne de la population lorsque la moyenne de la population n'est pas connue car elle a la même valeur attendue.
En statistique, la moyenne arithmétique est l'une des mesures idéales de la tendance centrale. Pour un ensemble donné d'observations, la moyenne arithmétique peut être calculée en ajoutant toutes les observations et en divisant la valeur obtenue par le nombre d'observations. Il y a deux types de moyenne, je.e. Moyenne d'échantillon et moyenne de population, qui est souvent utilisée dans les statistiques et la probabilité. La moyenne de l'échantillon est principalement utilisée pour estimer la moyenne de la population lorsque la moyenne de la population n'est pas connue car elle a la même valeur attendue.
Échantillon moyen implique la moyenne de l'échantillon dérivé de toute la population au hasard. Population signifie n'est rien d'autre que la moyenne de l'ensemble du groupe. Jetez un coup d'œil à cet article pour connaître les différences entre la moyenne de l'échantillon et la moyenne de la population.
Contenu: échantillon moyen vs moyenne de population
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Échantillon moyen | Population signifie |
|---|---|---|
| Signification | La moyenne de l'échantillon est la moyenne arithmétique des valeurs d'échantillon aléatoires tirées de la population. | La moyenne de la population représente la moyenne réelle de toute la population. |
| Symbole | x̄ (prononcé comme x bar) | μ (terme grec MU) |
| Calcul | Facile | Difficile |
| Précision | Faible | Haut |
| Écart-type | Lorsqu'il est calculé à l'aide de la moyenne de l'échantillon, est indiqué par (s). | Lorsqu'il est calculé en utilisant la moyenne de la population, est indiqué par (σ). |
Définition de la moyenne de l'échantillon
La moyenne de l'échantillon est la moyenne calculée à partir d'un groupe de variables aléatoires, tirée de la population. Il est considéré comme un estimateur efficace et impartial de la moyenne de la population, ce qui signifie que la valeur la plus attendue pour la statistique de l'échantillon est la statistique de la population, quelle que soit l'erreur d'échantillonnage. La moyenne de l'échantillon est calculée comme sous:
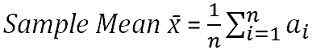 où, n = taille de l'échantillon
où, n = taille de l'échantillon
∑ = addition
unje = Toutes les observations
Définition de la moyenne de la population
Dans les statistiques, la moyenne de la population est définie comme la moyenne de tous les éléments de la population. C'est un moyen de caractéristique de groupe, où le groupe se réfère aux éléments de la population comme les articles, les personnes, etc. Et la caractéristique est l'élément d'intérêt. Comme la population est très grande et non connue, la moyenne de la population est inconnue constante. À l'aide de la formule suivante, la moyenne de la population peut être calculée,
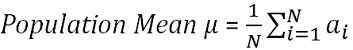 où n = taille de la population
où n = taille de la population
∑ = addition
unje = Toutes les observations
Différences clés entre la moyenne de l'échantillon et la moyenne de la population
Les différences significatives entre la moyenne de l'échantillon et la moyenne de la population sont expliquées en détail dans les points ci-dessous:
- La moyenne arithmétique des valeurs d'échantillon aléatoires tirées de la population est appelée moyenne de l'échantillon. La moyenne arithmétique de l'ensemble de la population est appelée moyenne de population.
- L'échantillon est représenté par X̄ (prononcé comme une barre X). En revanche, la moyenne de la population est étiquetée μ (terme grec MU).
- Alors que le calcul de la moyenne de l'échantillon est facile, car la liste des éléments fournies n'est que quelques-uns qui consomment très moins de temps. Par opposition à la moyenne de la population, où le calcul est difficile, car il existe de nombreux éléments dans la population qui prennent beaucoup de temps.
- La précision d'une moyenne de population est relativement supérieure à la moyenne de l'échantillon. La précision d'une moyenne d'échantillon peut être améliorée en augmentant le nombre d'observations.
- Les éléments de la population sont représentés par «n» dans la population moyenne. Au contraire, «n» en moyenne d'échantillon représente la taille de l'échantillon.
- Lorsque l'écart type est calculé à l'aide de la moyenne de l'échantillon, il est indiqué par la lettre «S». Inversement, lorsque la moyenne de la population est utilisée dans le calcul de l'écart type, il est représenté par Sigma (σ).
Conclusion
La méthode de calcul des deux moyens est la même, je.e. somme de toutes les observations divisées par le nombre d'observations, mais il y a une grande différence entre la façon dont elles sont représentées. Alors qu'une moyenne d'échantillon est écrite comme x̄ ou parfois m, la moyenne de la population est étiquetée μ. La moyenne de l'échantillon est une variable aléatoire tandis que la moyenne de la population est une constante inconnue.

