Différence entre la variance de l'échantillon et la variance de la population

Explication

Dans les statistiques, le terme échantillonnage fait référence à la sélection d'une partie des données statistiques agrégées dans le but d'obtenir des informations pertinentes sur l'ensemble. L'ensemble ou l'ensemble des informations statistiques sur un caractère particulier de tous les membres couverts par l'enquête est appelé «population» ou «univers». (Das, n.g., 2010). La partie sélectionnée de la population qui est utilisée pour obtenir les caractéristiques de la population ou de l'univers est appelée «échantillon». La population est considérée comme des unités ou des membres individuels, et certaines des unités sont incluses dans l'échantillon. Le nombre total d'unités de la population est appelée taille de la population, et celle de l'échantillon est appelée taille de l'échantillon. La population et l'échantillon peuvent être finis ou infinis et, de même, ils peuvent exister ou hypothétiques.

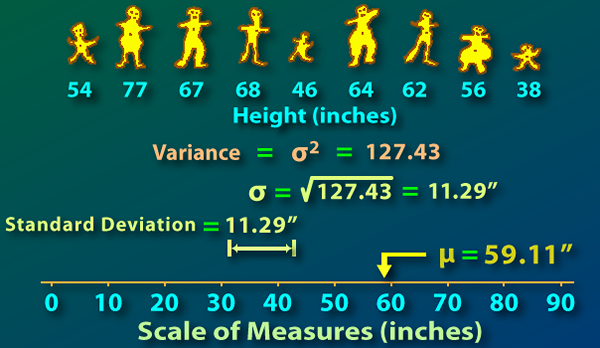
Variance: La variance est une valeur numérique qui montre à quel point les chiffres individuels d'un ensemble de données se répartissent sur la moyenne. C'est jusqu'où chaque nombre est de la moyenne, et donc les uns des autres. Une variance de la valeur zéro signifie que toutes les données sont identiques. Plus la variance, plus sont les valeurs réparties sur la moyenne, donc les unes des autres. Moins la variance, moins sont les valeurs réparties sur la moyenne, donc les unes des autres, et la variance ne peut pas être négative.

Différence entre la variance de la population et la variance de l'échantillon

La principale différence entre la variance de la population et la variance de l'échantillon concerne le calcul de la variance. La variance est calculée en cinq étapes. La première moyenne est calculée, puis nous calculons les écarts par rapport à la moyenne, et troisièmement, les écarts sont carrés, quatrièmement les écarts carrés sont résumés et finalement cette somme est divisée par le nombre d'éléments pour lesquels la variance est calculée. Ainsi, variance = σ (xi-x -) / n. Où xi = ith. Numéro, x- = moyenne et n = nombre d'éléments…

Maintenant, lorsque la variance doit être calculée à partir des données de la population, n est égal au nombre d'éléments. Ainsi, si la variance de la pression artérielle de toutes les 1000 personnes doit être calculée à partir des données sur les pressions sanguines de toutes les 1000 personnes, alors n = 1000. Cependant, lorsque la variance est calculée à partir des données d'échantillon 1 doit être déduite de N avant de diviser la somme des écarts carrés. Ainsi, dans l'exemple ci-dessus, si les données d'échantillons ont 100 éléments, le dénominateur serait de 100 - 1 = 99.

Pour cette raison, la valeur de variance calculée à partir des données d'échantillon est supérieure à la valeur qui aurait pu être trouvée en utilisant des données de population. La logique de le faire consiste à compenser notre manque d'informations sur les données de population. Il est impossible de trouver une variance des sommets dans les êtres humains, pour notre manque absolu d'informations sur les sommets de tous les êtres humains vivants, pour ne pas parler de l'avenir. Même si nous prenons un exemple modéré, comme les données de population sur les hauteurs de tous les hommes vivants en nous, il est physiquement possible, mais le coût et le temps impliqués dans ce domaine vaincraient le but de son calcul. C'est la raison pour laquelle des données d'échantillons sont prises pour la plupart des fins statistiques, et cela s'accompagne d'un manque d'informations sur la majorité des données. Afin de compenser cela, la valeur de la variance et de l'écart type, qui est une racine carrée de variance est plus élevée en cas de données d'échantillon que la variance des données de la population.

Cela agit comme un bouclier automatique pour les analystes et les décideurs. La logique s'applique aux décisions sur la budgétisation des capitaux, le financement personnel et commercial, la construction, la gestion du trafic et de nombreux domaines applicables. Cela aide le titulaire du pieu à être en toute sécurité tout en prenant une décision ou pour d'autres inférences.

Résumé: La variance de la population fait référence à la valeur de variance qui est calculée à partir des données de la population, et la variance de l'échantillon est la variance calculée à partir des données de l'échantillon. En raison de cette valeur du dénominateur dans la formule de variance en cas d'échantillon de données est «N-1», et c'est «N» pour les données de population. En conséquence, la variance et l'écart type dérivés des données d'échantillon sont plus que ceux trouvés à partir des données de population.