Différence entre la séquence et la série

- 5067
- 1613
- Lena Muller
 En mathématiques et en statistiques, la ligne qui délimite la séquence et les séries sont minces et floues, à cause de laquelle beaucoup pensent que ces termes sont une seule et même chose. Néanmoins, la notion de séquence diffère des séries dans le sens séquence fait référence à un arrangement dans l'ordre particulier dans lequel les termes connexes se suivent, je.e. Il a une première unité, une deuxième unité, une troisième unité identifiée et ainsi de suite.
En mathématiques et en statistiques, la ligne qui délimite la séquence et les séries sont minces et floues, à cause de laquelle beaucoup pensent que ces termes sont une seule et même chose. Néanmoins, la notion de séquence diffère des séries dans le sens séquence fait référence à un arrangement dans l'ordre particulier dans lequel les termes connexes se suivent, je.e. Il a une première unité, une deuxième unité, une troisième unité identifiée et ainsi de suite.
Lorsqu'une séquence suit une règle particulière, elle s'appelle comme progression. Ce n'est pas exactement la même que série qui est défini comme la sommation des éléments d'une séquence. Prenez une lecture de l'article pour connaître la différence significative entre la séquence et la série.
Contenu: séquence vs série
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Séquence | Série |
|---|---|---|
| Signification | La séquence est décrite comme l'ensemble de nombres ou d'objets qui suit un certain motif. | La série se réfère à la somme des éléments de la séquence. |
| Commande | Important | Parfois important |
| Exemple | 1, 3, 5, 7, 9, 11… n… | 1 + 3 + 5 + 9 + 11… n… |
Définition de la séquence
En mathématiques, un ensemble ordonné d'objets ou de nombres, comme un1, un2, un3, un4, un5, un6… unn… . seraient dans une séquence, si, selon une règle, a une valeur définie. Les membres de la séquence sont appelés terme ou élément qui est égal à toute valeur du nombre naturel. Chaque terme d'une séquence est lié au terme précédent et suivant. En général, les séquences ont des règles ou un modèle cachés, ce qui vous aide à trouver la valeur du terme suivant.
Le nième terme est la fonction de l'entier n (positif), considéré comme le terme général de la séquence. Une séquence peut être finie ou infinie.
- Séquence finie: Une séquence finie est celle qui s'arrête à la fin de la liste des nombres a1, un2, un3, un4, un5, un6… unn, est représenté par:
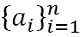
- Séquence infinie: Une séquence infinie fait référence à une séquence sans fin, un1, un2, un3, un4, un5, un6… unn… .., est représenté par:
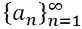
Définition des séries
L'ajout des termes d'une séquence (unn), est connu sous le nom de série. Comme la séquence, les séries peuvent également être finies ou infinies, où une série finie est celle qui a un nombre fini de termes écrits comme un1 + un2 + un3 + un4 + un5 + un6 + … unn. Contrairement aux séries infinies, où le nombre d'éléments n'est pas fini ou qui ne sont pas en fin, écrit comme un1 + un2 + un3 + un4 + un5 + un6 + … unn +… .
Si un1 + un2 + un3 + un4 + un5 + un6 + … unn = Sn, puis sn est considéré comme la somme des n éléments de la série. La somme des termes est souvent représentée par la lettre grecque Sigma (ʃ). Ainsi,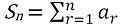
Différences clés entre la séquence et les séries
La différence entre la séquence et la série peut être clairement tracée sur les motifs suivants:
- La séquence est définie comme la collection de nombres ou d'objets qui suivent un modèle définitif. Lorsque les éléments de la séquence sont ajoutés, ils sont connus sous le nom de série.
- L'ordre compte dans une séquence, car il existe une certaine règle qui prescrit le modèle de la séquence. Par conséquent, 1, 2, 3Tre est différent de 3, 1, 2. D'un autre côté, dans une série, l'ordre d'apparence peut ou non, comme dans le cas d'une série absolument convergente, l'ordre n'a pas d'importance. Ainsi, 1 + 2 + 3 est le même que 3 + 1 + 2, seule leur séquence est différente.
Conclusion
Progression arithmétique (un.P.) et la progression géométrique (g.P.) sont aussi des séquences, pas des séries. La progression arithmétique est une séquence dans laquelle il existe une différence commune entre les termes consécutifs tels que 2, 4, 6, 8 et ainsi. Au contraire, dans une progression géométrique, chaque élément de la séquence est le multiple commun du terme précédent tel que 3, 9, 27, 81 et ainsi. De même, la séquence de Fibonacci est également l'une des séquences infinies populaires, dans lesquelles chaque terme est obtenu en additionnant les deux termes précédents 1, 1, 3, 5, 8, 13, 21 et ainsi de suite.

