Différence entre le test t et le test F

- 904
- 62
- Mathilde Roux
 Les tests d'hypothèse commence par la configuration des locaux, qui est suivi par la sélection d'un niveau de signification. Ensuite, nous devons choisir la statistique de test, je.e. T-test ou test F. Alors que test t est utilisé pour comparer deux échantillons connexes, test F est utilisé pour tester l'égalité de deux populations.
Les tests d'hypothèse commence par la configuration des locaux, qui est suivi par la sélection d'un niveau de signification. Ensuite, nous devons choisir la statistique de test, je.e. T-test ou test F. Alors que test t est utilisé pour comparer deux échantillons connexes, test F est utilisé pour tester l'égalité de deux populations.
L'hypothèse est une proposition simple qui peut être prouvée ou réfutée par diverses techniques scientifiques et établit la relation entre indépendant et une variable dépendante. Il est capable d'être testé et vérifié pour déterminer sa validité, par un examen impartial. Le test d'une hypothèse tente de préciser, si la supposition est valide ou non.
Pour un chercheur, il est impératif de choisir le bon test pour son hypothèse car la décision entière de valider ou de refuser l'hypothèse nulle est basée sur elle. Prenez une lecture de l'article donné pour comprendre la différence entre le test t et le test F.
Contenu: T-Test vs F-test
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Test t | Test F |
|---|---|---|
| Signification | Le test t est un test d'hypothèse univarié, qui est appliqué lorsque l'écart type n'est pas connu et que la taille de l'échantillon est petite. | Le test F est un test statistique, qui détermine l'égalité des variances des deux populations normales. |
| Statistique de test | La statistique T suit l'étudiant en T-distribution, sous une hypothèse nulle. | La statistique F suit Snedecor F-Distribution, sous une hypothèse nulle. |
| Application | Comparaison des moyens de deux populations. | Comparaison de deux écarts de population. |
Définition du test t
Un test t est une forme du test d'hypothèse statistique, basée sur la statistique T de l'élève et la distribution en T pour découvrir la valeur p (probabilité) qui peut être utilisée pour accepter ou rejeter l'hypothèse nulle.
Analyses des tests en T Si les moyens de deux ensembles de données sont très différents les uns des autres, je.e. Que la moyenne de la population soit égale ou différente de la moyenne standard. Il peut également être utilisé pour vérifier si la ligne de régression a une pente différente de zéro. Le test repose sur un certain nombre d'hypothèses, qui sont:
- La population est infinie et normale.
- La variance de la population est inconnue et estimée à partir de l'échantillon.
- La moyenne est connue.
- Les échantillons d'observations sont aléatoires et indépendants.
- La taille de l'échantillon est petite.
- H0 Peut être unilatéral ou deux côtés.
L'écart moyen et type des deux échantillons sont utilisés pour faire la comparaison entre eux, de sorte que:
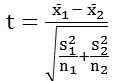 où,
où,
X1 = Moyenne du premier ensemble de données
x̄2 = moyenne du deuxième ensemble de données
S1 = Écart-type du premier ensemble de données
S2 = Écart-type du deuxième ensemble de données
n1 = Taille du premier ensemble de données
n2 = Taille du deuxième ensemble de données
Définition du test F
Le test F est décrit comme un type de test d'hypothèse, basé sur la distribution F Snedecor, sous l'hypothèse nulle. Le test est effectué lorsqu'on ne sait pas si les deux populations ont la même variance.
Le test F peut également être utilisé pour vérifier si les données sont conformes à un modèle de régression, qui est acquise par analyse le moins carré. En cas d'analyse de régression linéaire multiple, il examine la validité globale du modèle ou détermine si l'une des variables indépendantes a une relation linéaire avec la variable dépendante. Un certain nombre de prédictions peuvent être faites, la comparaison des deux ensembles de données. L'expression de la valeur de test F est dans le rapport des variances des deux observations, qui est montrée comme sous:
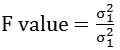 Où, σ2 = variance
Où, σ2 = variance
Les hypothèses sur lesquelles les tests F repose sont:
- La population est normalement distribuée.
- Les échantillons ont été prélevés au hasard.
- Les observations sont indépendantes.
- H0 Peut être unilatéral ou deux côtés.
Différences clés entre le test t et le test F
La différence entre le test t et le test F peut être clairement tracée sur les motifs suivants:
- Un test d'hypothèse univarié qui est appliqué lorsque l'écart type n'est pas connu et que la taille de l'échantillon est petite est un test t. D'un autre côté, un test statistique, qui détermine l'égalité des variances des deux ensembles de données normaux, est connu sous le nom de test F.
- Le test t est basé sur la statistique T suit l'étudiant t-distribution, sous l'hypothèse nulle. Inversement, la base du test F est la statistique F suit Snedecor F-Distribution, sous l'hypothèse nulle.
- Le test t est utilisé pour comparer les moyens de deux populations. En revanche, le test F est utilisé pour comparer deux variances de population.
Conclusion
Le test t et le test F sont les deux, du nombre de différents types de test statistique utilisés pour les tests d'hypothèse et décident si nous allons accepter l'hypothèse nulle ou la rejeter. Le test d'hypothèse ne prend pas de décisions elle-même, mais plutôt le chercheur dans la prise de décision.
- « Différence entre le test paramétrique et non paramétrique
- Différence entre la variance et l'écart type »

