Différence entre le test t et le test z

- 1564
- 181
- Elisa Petit
 Test t fait référence à un test d'hypothèse univarié basé sur la statistique T, dans laquelle la moyenne est connue, et la variance de la population est approximée de l'échantillon. D'autre part, Test z est également un test univarié basé sur une distribution normale standard.
Test t fait référence à un test d'hypothèse univarié basé sur la statistique T, dans laquelle la moyenne est connue, et la variance de la population est approximée de l'échantillon. D'autre part, Test z est également un test univarié basé sur une distribution normale standard.
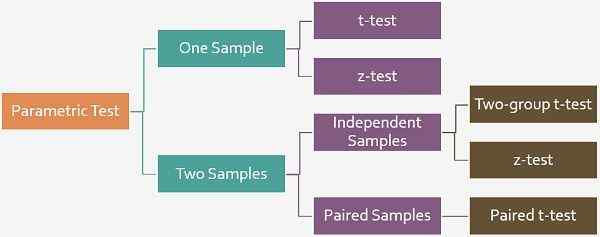
En termes simples, une hypothèse fait référence à une supposition qui doit être acceptée ou rejetée. Il y a deux procédures de test d'hypothèse, je.e. test paramétrique et test non paramétrique, dans lequel le test paramétrique est basé sur le fait que les variables sont mesurées sur une échelle d'intervalle, tandis que dans le test non paramétrique, il en va de même pour être mesuré sur une échelle ordinale. Maintenant, dans le test paramétrique, il peut y avoir deux types de test, de test t et de test Z.
Cet article vous donnera une compréhension de la différence entre le test t et le test Z en détail.
Contenu: T-test vs z-test
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
| Base de comparaison | Test t | Test z |
|---|---|---|
| Signification | Le test t fait référence à un type de test paramétrique appliqué pour identifier, comment les moyens de deux ensembles de données diffèrent les uns des autres lorsque la variance n'est pas donnée. | Le test Z implique un test d'hypothèse qui vérifie si les moyens de deux ensembles de données sont différents les uns des autres lorsque la variance est donnée. |
| Basé sur | Distribution étudiante-T | Distribution normale |
| Écart de population | Inconnu | Connu |
| Taille de l'échantillon | Petit | Grand |
Définition du test t
Un test t est un test d'hypothèse utilisé par le chercheur pour comparer les moyens de population pour une variable, classifiée en deux catégories en fonction de la variable d'intervalle moins que. Plus précisément, un test t est utilisé pour examiner comment les moyens prélevés de deux échantillons indépendants diffèrent.
Le test t suit la distribution t, ce qui est approprié lorsque la taille de l'échantillon est petite, et l'écart type de population n'est pas connu. La forme d'une distribution t est fortement affectée par le degré de liberté. Le degré de liberté implique le nombre d'observations indépendantes dans un ensemble donné d'observations.
Hypothèses de test t:
- Tous les points de données sont indépendants.
- La taille de l'échantillon est petite. Généralement, une taille d'échantillon dépassant 30 unités d'échantillon est considérée comme grande, sinon petite mais qui ne devrait pas être inférieure à 5, pour appliquer le test t.
- Les valeurs d'échantillons doivent être prélevées et enregistrées avec précision.
La statistique de test est:
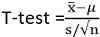
x ̅ est la moyenne de l'échantillon
S est un échantillon d'écart type
n est la taille de l'échantillon
μ est la moyenne de la population
T-test apparié: Un test statistique appliqué lorsque les deux échantillons sont dépendants et que des observations appariées sont prises.
Définition du test Z
Le test Z fait référence à une analyse statistique univariée utilisée pour tester l'hypothèse selon laquelle les proportions de deux échantillons indépendants diffèrent considérablement. Il détermine dans quelle mesure un point de données est loin de sa moyenne de l'ensemble de données, en écart-type.
Le chercheur adopte un test z, lorsque la variance de la population est connue, en substance, lorsqu'il y a une grande taille d'échantillon, la variance de l'échantillon est considérée comme étant approximativement égale à la variance de la population. De cette façon, il est supposé être connu, malgré le fait que seules des données d'échantillons sont disponibles et que un test normal peut être appliqué.
Hypothèses de test z:
- Toutes les observations d'échantillons sont indépendantes
- La taille de l'échantillon doit dépasser 30.
- La distribution de z est normale, avec un zéro moyen et une variance 1.
La statistique de test est:
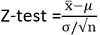
x ̅ est la moyenne de l'échantillon
σ est l'écart type de population
n est la taille de l'échantillon
μ est la moyenne de la population
Différences clés entre le test t et le test Z
La différence entre le test t et le test Z peut être clairement tracée sur les motifs suivants:
- Le test t peut être compris comme un test statistique qui est utilisé pour comparer et analyser si les moyens des deux populations sont différents ou non lorsque l'écart type n'est pas connu. CONTRE, Z-TEST est un test paramétrique, qui est appliqué lorsque l'écart type est connu, pour déterminer, si les moyennes des deux ensembles de données diffèrent les uns des autres.
- Le test t est basé sur la distribution T de l'étudiant. Au contraire, le test Z repose sur l'hypothèse que la distribution des moyennes d'échantillon est normale. La distribution en T de l'étudiant et la distribution normale se semblent similaires, car les deux sont symétriques et en forme de cloche. Cependant, ils diffèrent dans le sens où dans une distribution en T, il y a moins d'espace au centre et plus dans la queue.
- L'une des conditions importantes pour adopter le test t est que la variance de la population est inconnue. Inversement, la variance de la population doit être connue ou supposée être connue en cas de test Z.
- Le test z est utilisé lorsque la taille de l'échantillon est grande, je.e. n> 30, et le test t est approprié lorsque la taille de l'échantillon est petite, dans le sens où n < 30.
Conclusion
Dans l'ensemble, le test t et le test Z sont des tests presque similaires, mais les conditions de leur application sont différentes, ce qui signifie que le test t est approprié lorsque la taille de l'échantillon ne dépasse pas 30 unités. Cependant, s'il est plus de 30 unités, le test Z doit être effectué. De même, il existe d'autres conditions, ce qui indique clairement que le test doit être effectué dans une situation donnée.
- « Différence entre l'assurance incendie et l'assurance maritime
- Différence entre l'audit et l'examen »

