Différence entre l'union et l'intersection

Avant de comprendre la différence entre le syndicat des deux opérateurs de sets et l'intersection, comprenons d'abord le concept de théorie des ensembles. La théorie des ensembles est une branche fondamentale des mathématiques que les études d'études, en particulier si un objet appartient ou n'appartient pas à un ensemble d'objets qui sont en quelque sorte des mathématiques pertinentes. Set est essentiellement une collection d'objets bien définis, qui peuvent ou non être de pertinence mathématique, tels que les nombres ou les fonctions. Les objets dans un ensemble sont appelés éléments, qui peuvent être des nombres, des personnes, des voitures, des états, etc. Presque n'importe quoi et n'importe quel nombre d'éléments peuvent être collectés ensemble pour créer un ensemble.

En termes simples, Set est une collection de n'importe quel nombre d'éléments non ordonnés qui peuvent être considérés comme un seul objet dans son ensemble. Comprenons les concepts de base et la notation d'un ensemble et comment il est représenté. Tout commence par une relation binaire entre un objet x et un ensemble a. Pour représenter si x est membre d'un ensemble A, la notation x ∊ a est utilisée, tandis que x ∉ a indique que l'objet x n'appartient pas à l'ensemble A. Le membre d'un ensemble est répertorié dans des accolades bouclées. Par exemple, l'ensemble des nombres premiers de moins de 10 peut être écrit comme 2, 3, 5, 7. De même, un ensemble de nombres pair inférieurs à 10 peut être écrit comme 2, 4, 6, 8. Hypothétiquement, presque tout ensemble fini peut être représenté par ses membres.

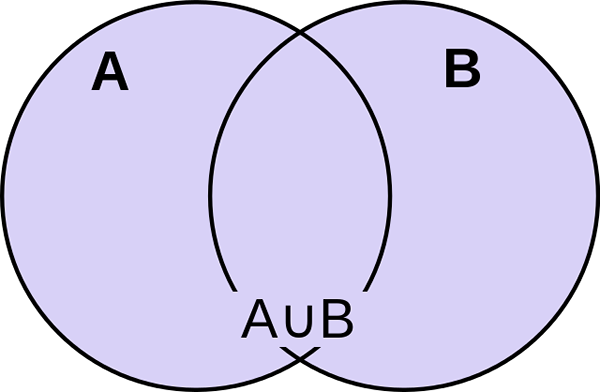
Qu'est-ce que l'union des ensembles?

L'union de deux ensembles A et B est définie comme l'ensemble des éléments qui appartiennent à A ou B, ou peut-être les deux. Il est simplement défini comme l'ensemble de tous les éléments ou membres distincts, où les membres appartiennent à l'un de ces ensembles. L'opérateur syndical correspond à la logique ou et est représentée par le symbole ∪. C'est le plus petit ensemble contenant tous les éléments des deux ensembles. Par exemple, si le jeu a est 1, 2, 3, 4, 5 et que le jeu B est 3, 4, 6, 7, 9, alors l'union de A et B est représentée par A∪b et est écrite comme 1, 2, 3, 4, 5, 6, 7, 9. Comme les numéros 3 et 4 sont présents dans les ensembles A et B, il n'est pas nécessaire de les énumérer deux fois. Il est évident que le nombre d'éléments de l'Union de A et B est plus petit que la somme des ensembles individuels, car peu de chiffres sont communs dans les deux ensembles.

A = 1, 3, 5, 7, 9

B = 3, 6, 9, 12, 15

A∪b = 1, 3, 5, 6, 7, 9, 12, 15

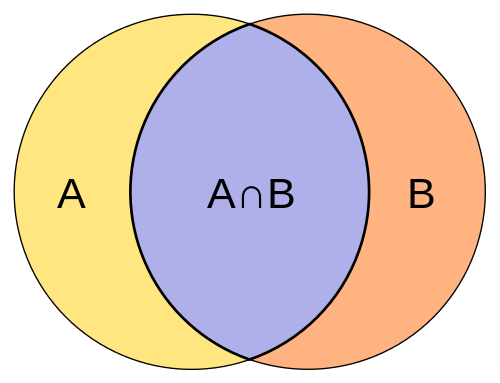
Qu'est-ce que l'intersection des ensembles?

L'intersection de deux ensembles A et B est définie comme l'ensemble des éléments qui appartiennent à la fois à A et B. Il est simplement défini comme l'ensemble contenant tous les éléments de l'ensemble A qui appartiennent également à l'ensemble B, et de même tous les éléments de l'ensemble B appartiennent à l'ensemble A. L'opérateur d'intersection correspond à la logique et et est représentée par le symbole ∩. Au contraire, l'intersection de deux ensembles est le plus grand ensemble contenant tous les éléments communs aux deux ensembles. Par exemple, si le jeu a est 1, 2, 3, 4, 5 et que le jeu B est 3, 4, 6, 7, 9, alors l'intersection de A et B est représentée par A∩b et est écrite comme 3, 4. Comme seuls les nombres 3 et 4 sont communs dans les deux ensembles A et B, ils sont appelés l'intersection des ensembles.

A = 2, 3, 5, 7, 11

B = 1, 3, 5, 7, 9, 11

A∩b = 3, 5, 7, 11

Différence entre l'union et l'intersection des ensembles

1. Basique - L'union de deux ensembles A et B est définie comme l'ensemble des éléments qui appartiennent à A ou B, ou peut-être les deux, tandis que l'intersection de deux ensembles est définie comme l'ensemble des éléments appartenant à la fois à A et B.
2. Représentation symbolique - L'union de deux ensembles est représentée par le symbole «∪», tandis que l'intersection de deux ensembles est représentée par le symbole «∩».
3. Pertinence logique - L'union de deux ensembles correspond à la logique «ou» tandis que l'intersection de deux ensembles correspond à la logique «et» logique.
4. Exemple - Soit a = a, e, i, o, u et

B = a, b, c, d, e, f

A∪b = a, b, c, d, e, f, i, o, u

A∩b = a, e

Union vs. Intersection: graphique de comparaison

Résumé de l'Union vs. Intersection

L'union et l'intersection sont les deux opérations fondamentales par lesquelles les ensembles peuvent être combinés et liés les uns aux autres. En termes de théorie des ensembles, Union est l'ensemble de tous les éléments qui sont dans les deux ensembles, soit dans les deux, tandis que l'intersection est l'ensemble de tous les éléments distincts qui appartiennent aux deux ensembles. L'union de deux ensembles A et B est symbolisée comme «a∪b», tandis que l'intersection de A et B est symbolisée comme «a∩b». L'ensemble n'est rien d'autre qu'une collection d'objets bien définis, tels que les nombres et les fonctions, et les objets d'un ensemble sont appelés éléments.