Différences entre la corrélation et la régression

La corrélation et la régression sont des outils statistiques qui traitent de deux variables ou plus. Bien que les deux se rapportent au même sujet, il existe des différences entre les deux. Les différences, entre les deux, sont expliquées ci-dessous.

Signification

Le terme corrélation par rapport à deux ou plusieurs variables signifie que les variables sont liées d'une manière ou d'une autre. L'analyse de corrélation détermine s'il existe une relation entre deux variables et la force de la relation. Si deux variables x (indépendantes) et y (dépendantes) sont si liées que la variation de l'ampleur de la variable indépendante est accompagnée, par variation d'ampleur de la variable dépendante, les deux variables seraient corrélées.

La corrélation peut être linéaire ou non linéaire. Une corrélation linéaire est celle où les variables sont si liées que le changement de la valeur d'une variable entraînerait une modification de la valeur d'une autre variable de manière cohérente. Dans une corrélation linéaire, les points dispersés liés aux valeurs respectives des variables dépendantes et indépendantes se regrouperaient autour d'une ligne droite non horizontale, bien qu'une ligne droite horizontale indique également une relation linéaire entre les variables si une ligne droite pouvait relier les points représentant représentant les variables.

L'analyse de régression, en revanche, utilise les données existantes pour déterminer une relation mathématique entre les variables qui peuvent être utilisées pour déterminer la valeur de la variable dépendante par rapport à toute valeur de la variable indépendante.

Orientation statistique

La corrélation concerne la mesure de la force de l'association ou de l'intensité de la relation, alors que la régression concerne la prédiction de la valeur de la variable dépendante par rapport à une valeur connue de la variable indépendante. Cela peut être expliqué avec les formules suivantes.

La corrélation de corrélation ou la corrélation du coefficient (R) entre X & Y se trouve avec la formule suivante;

r = covariance (x, y) / σx.σy, cov (x, y) = σxy / n - (σx / n) (σy / n), σx & σy sont des écarts-types de x et y respectivement et, -1 < r 0, then correlation coefficient between x and y = correlation coefficient between u and v.

Le coefficient de corrélation R est un nombre pur et indépendant de l'unité de mesure. Ainsi, si x est de la hauteur (pouces) et y est du poids (lbs.) des personnes d'une certaine région, alors r n'est ni en pouces ni en lbs., mais simplement un nombre.

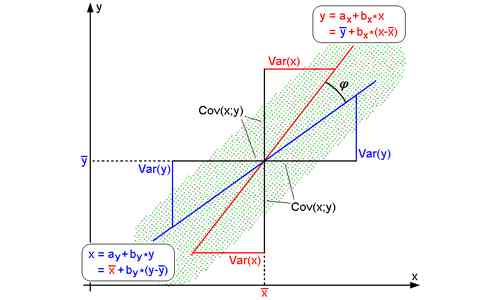
L'équation de régression se trouve avec la formule suivante;

L'équation de régression de y sur x (pour découvrir l'estimation de y) est y - y '= byx (x-x‾), Byx est appelé coefficient de régression de y sur x. L'équation de régression de x sur y (pour découvrir l'estimation de x) est x - x '= bxy (y-y‾), bxy est appelé coefficient de régression de x sur y.

L'analyse de corrélation n'assume pas la dépendance d'aucune variable sur d'autres variables, elle n'essaie pas non plus de découvrir la relation entre les deux. Il estime simplement le degré d'association entre les variables. En d'autres termes, l'analyse de corrélation teste l'interdépendance des variables. L'analyse de régression en revanche décrit la dépendance de la variable dépendante ou de la variable de réponse de la variable / s indépendante ou explicative. L'analyse de régression suppose qu'il existe une relation causale unidirectionnelle entre les variables explicatives et de réponse, et ne prend pas en compte si cette relation causale est positive ou négative. Pour la corrélation, les deux valeurs des variables dépendantes et indépendantes sont aléatoires, mais pour les valeurs de régression des variables indépendantes ne doivent pas être aléatoires.

Résumé

1. L'analyse de corrélation est un test d'interdépendance entre deux variables. L'analyse de régression donne une formule mathématique pour déterminer la valeur de la variable dépendante par rapport à une valeur de variable indépendante / s.

2. Le coefficient de corrélation est indépendant du choix d'origine et d'échelle, mais le coefficient de régression n'est pas ainsi.

Pour la corrélation, les valeurs des deux variables doivent être aléatoires, mais ce n'est pas le cas pour le coefficient de régression.

Bibliographie

1. Das, n. g., (1998), Méthodes statistiques, Calcutta

2. Corrélation et régression, disponible sur www.le.CA.UK / BL / GAT / VirtualFC / Statistiques / régression

3. Régression et corrélation, disponible sur www.abîme.uoregon.édu