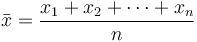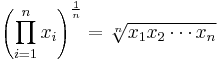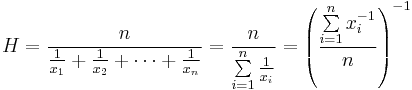Mean Vs. Médian

- 1352
- 7
- Lena Pons
Moyenne (ou moyen) et médian sont des termes statistiques qui ont un rôle quelque peu similaire en termes de compréhension tendance centrale d'un ensemble de scores statistiques. Bien qu'une moyenne ait traditionnellement été une mesure populaire d'un point médian dans un échantillon, il a l'inconvénient d'être affecté par une seule valeur trop élevée ou trop faible par rapport au reste de l'échantillon. C'est pourquoi une médiane est parfois considérée comme une meilleure mesure d'un point médian.
Tableau de comparaison
| Moyenne | Médian | |
|---|---|---|
| Définition | La moyenne est la moyenne arithmétique d'un ensemble de nombres ou de distribution. C'est la mesure la plus couramment utilisée de la tendance centrale d'un ensemble de nombres. | La médiane est décrite comme la valeur numérique séparant la moitié plus élevée d'un échantillon, d'une population ou d'une distribution de probabilité, de la moitié inférieure. |
| Applicabilité | La moyenne est utilisée pour les distributions normales. | La médiane est généralement utilisée pour les distributions asymétriques. |
| Pertinence pour l'ensemble de données | La moyenne n'est pas un outil robuste car il est largement influencé par les valeurs aberrantes. | La médiane est mieux adaptée aux distributions asymétriques à dériver à la tendance centrale car elle est beaucoup plus robuste et sensée. |
| Comment calculer | Une moyenne est calculée en additionnant toutes les valeurs et en divisant ce score par le nombre de valeurs. | La médiane est le nombre trouvé au milieu exact de l'ensemble de valeurs. Une médiane peut être calculée en répertoriant tous les nombres dans l'ordre croissant, puis en localisant le numéro au centre de cette distribution. |
Définitions de la moyenne et de la médiane
En mathématiques et en statistiques, la moyenne ou le moyenne arithmétique d'une liste de nombres est la somme de la liste entière divisée par le nombre d'éléments dans la liste. Lorsque vous regardez les distributions symétriques, la moyenne est probablement la meilleure mesure pour arriver à Central Tendance. Dans la théorie des probabilités et les statistiques, un médian ce nombre séparait la moitié plus élevée d'un échantillon, d'une population ou d'une distribution de probabilité, de la moitié inférieure.
Comment calculer
Le Moyenne ou la moyenne est probablement la méthode la plus couramment utilisée pour décrire la tendance centrale. Une moyenne est calculée en additionnant toutes les valeurs et en divisant ce score par le nombre de valeurs. Le moyenne arithmétique d'un échantillon 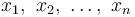 est la somme des valeurs échantillonnées divisées par le nombre d'éléments dans l'échantillon:
est la somme des valeurs échantillonnées divisées par le nombre d'éléments dans l'échantillon:
Le Médian est le nombre trouvé au milieu exact de l'ensemble de valeurs. Une médiane peut être calculée en répertoriant tous les nombres dans l'ordre croissant, puis en localisant le numéro au centre de cette distribution. Ceci s'applique à une liste de nombres impairs; En cas de nombre uniforme d'observations, il n'y a pas de valeur moyenne unique, c'est donc une pratique habituelle pour prendre la moyenne des deux valeurs moyennes.
Exemple
Disons qu'il y a neuf étudiants dans une classe avec les scores suivants sur un test: 2, 4, 5, 7, 8, 10, 12, 13, 83. Dans ce cas, le score moyen (ou le moyenne) est la somme de tous les scores divisés par neuf. Cela fonctionne à 144/9 = 16. Notez que même si 16 est la moyenne arithmétique, elle est déformée par le score inhabituellement élevé de 83 par rapport aux autres scores. Presque tous les scores des étudiants sont dessous la moyenne. Par conséquent, dans ce cas, la moyenne n'est pas un bon représentant tendance centrale de cet échantillon.
Le médian, D'un autre côté, est la valeur qui est telle que la moitié des scores sont supérieurs et la moitié des scores ci-dessous. Donc, dans cet exemple, la médiane est 8. Il y a quatre scores ci-dessous et quatre au-dessus de la valeur 8. Ainsi 8 représente le point médian ou la tendance centrale de l'échantillon.
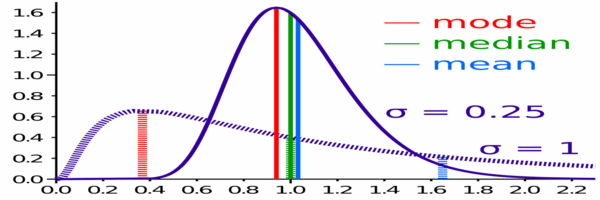 Comparaison de la moyenne, de la médiane et du mode de deux distributions log-normales avec une asymétrie différente.
Comparaison de la moyenne, de la médiane et du mode de deux distributions log-normales avec une asymétrie différente. Inconvénients des moyens arithmétiques et des médianes
La moyenne n'est pas un outil statistique robuste car il ne peut pas être appliqué à toutes les distributions, mais est facilement l'outil statistique le plus utilisé pour dériver la tendance centrale. La raison pour laquelle la moyenne ne peut pas être appliquée à toutes.
L'inconvénient de la médiane est qu'il est difficile de gérer théoriquement. Il n'y a pas de formule mathématique facile pour calculer la médiane.
Autres types de moyens
Il existe de nombreuses façons de déterminer la tendance centrale, ou moyenne, d'un ensemble de valeurs. La moyenne discutée ci-dessus est techniquement la moyenne arithmétique et est la statistique la plus couramment utilisée pour la moyenne. Il existe d'autres types de moyens:
Moyenne géométrique
La moyenne géométrique est définie comme le nla racine du produit de n chiffres, je.e., pour un ensemble de nombres X1,X2,… ,Xn, la moyenne géométrique est définie comme
Les moyens géométriques sont meilleurs que les moyens arithmétiques pour décrire la croissance proportionnelle. Par exemple, une bonne application pour la moyenne géométrique est le calcul du taux de croissance annuel composé (TCAC).
Moyenne harmonique
La moyenne harmonique est la réciproque de la moyenne arithmétique des réciproques. La moyenne harmonique H des nombres réels positifs X1,X2,… ,Xn est
Une bonne application pour les moyens harmoniques est quand la moyenne des multiples. Pour les exampes, il est préférable d'utiliser la moyenne harmonique pondérée lors du calcul du rapport prix-bénéfice (P / E). Si les rapports P / E sont moyennés en utilisant une moyenne arithmétique pondérée, les points de données élevés obtiennent des poids indûment plus grands que les points de données faibles.
Pythagorean signifie
La moyenne arithmétique, la moyenne géométrique et la moyenne harmonique forment ensemble un ensemble de moyens appelés les moyens pythagoriques. Pour tout ensemble de nombres, la moyenne harmonique est toujours la plus petite de tous les moyens pythagoriques, et la moyenne arithmétique est toujours la plus grande des 3 moyens. je.e. Moyenne harmonique ≤ moyenne géométrique ≤ moyenne arithmétique.
Autres significations des mots
Moyenne peut être utilisé comme figure de la parole et détient une référence littéraire. Il est également utilisé pour impliquer pauvre ou non. Médian, Dans une référence géométrique, est une ligne droite passant d'un point du triangle au centre du côté opposé.