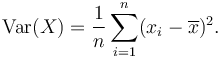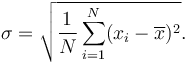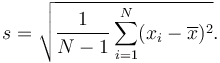Écart-type vs. Variance

- 4813
- 1379
- Adrien Jean
Écart-type et variance sont des mesures statistiques de la dispersion des données, i.e., Ils représentent la variation de la moyenne, ou dans quelle mesure les valeurs "s'écartent généralement" de la moyenne (moyenne). Une variance ou un écart-type de zéro indique que toutes les valeurs sont identiques.
La variance est la moyenne des carrés des écarts (i.e., différence de valeurs par rapport à la moyenne), et l'écart type est la racine carrée de cette variance. L'écart type est utilisé pour identifier les valeurs aberrantes des données.
Tableau de comparaison
Différences - similitudes -| Écart-type | Variance | |
|---|---|---|
| Formule mathématique | Racine carrée de variance | Moyenne des carrés d'écarts de chaque valeur par rapport à la moyenne dans un échantillon. |
| Symbole | Lettre grecque Sigma - σ | Aucun symbole dédié; exprimé en termes d'écart type ou d'autres valeurs. |
| Valeurs concernant l'ensemble de données donné | Même échelle que les valeurs dans l'ensemble de données donné; Par conséquent, exprimé dans les mêmes unités. | Échelle supérieure aux valeurs de l'ensemble de données donné; non exprimé dans la même unité que les valeurs elles-mêmes. |
| Les valeurs sont-elles négatives ou positives? | Toujours non négatif | Toujours non négatif |
| Application du monde réel | Échantillonnage de la population; Identifier les valeurs aberrantes | Formules statistiques, financement. |
Concepts importants
- Moyenne: la moyenne de toutes les valeurs dans un ensemble de données (ajoutez toutes les valeurs et divisez leur somme par le nombre de valeurs).
- Déviation: la distance de chaque valeur de la moyenne. Si la moyenne est de 3, une valeur de 5 a un écart de 2 (soustrayez la moyenne de la valeur). La déviation peut être positive ou négative.
Symboles
La formule de l'écart-type et de la variance est souvent exprimée en utilisant:
- x̅ = la moyenne, ou la moyenne, de tous les points de données du problème
- X = un point de données individuel
- N = le nombre de points dans l'ensemble de données
- ∑ = la somme des [carrés des écarts]
Formules
La variance d'un ensemble de n Des valeurs tout aussi probables peuvent être écrites comme:
L'écart type est la racine carrée de la variance:
Les formules avec des lettres grecques ont une façon de paraître intimidante, mais cela moins compliqué qu'il n'y paraît. Pour le mettre en étapes simples:
- Trouvez la moyenne de tous les points de données
- Découvrez jusqu'où chaque point est loin de la moyenne (c'est l'écart)
- carré chaque déviation (je.e. la différence de chaque valeur de la moyenne)
- Divisez la somme des carrés par le nombre de points.
Qui donne la variance. Prenez la racine carrée de la variance pour trouver l'écart type.
Cette excellente vidéo de Khan Academy explique les concepts de variance et d'écart type:
Exemple
Disons qu'un ensemble de données comprend la hauteur de six pissenlits: 3 pouces, 4 pouces, 5 pouces, 4 pouces, 11 pouces et 6 pouces.
Tout d'abord, trouvez la moyenne des points de données: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Donc la hauteur moyenne est 5.5 pouces. Maintenant, nous avons besoin des écarts, nous trouvons donc la différence de chaque plante par rapport à la moyenne: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Maintenant carré chaque déviation et trouvez leur somme: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Divisez maintenant la somme des carrés par le nombre de points de données, dans ce cas, les usines: 43.5/6 = 7.25
Ainsi, la variance de cet ensemble de données est 7.25, qui est un nombre assez arbitraire. Pour le convertir en une mesure du monde réel, prenez la racine carrée de 7.25 pour trouver l'écart type en pouces.
L'écart type est d'environ 2.69 pouces. Cela signifie que pour l'échantillon, tout pissenlit dans les 2.69 pouces de la moyenne (5.5 pouces) est «normal».
Pourquoi carré les écarts?
Les écarts sont carrés pour empêcher les valeurs négatives (écarts inférieurs à la moyenne) pour annuler les valeurs positives. Cela fonctionne parce qu'un nombre négatif est une valeur positive. Si vous aviez un ensemble de données simples avec des écarts par rapport à la moyenne de +5, +2, -1 et -6, la somme des écarts sera nul si les valeurs ne sont pas carrées (i.e. 5 + 2 - 1 - 6 = 0).
Applications du monde réel
La variance est exprimée comme une dispersion mathématique. Puisqu'il s'agit d'un nombre arbitraire par rapport aux mesures d'origine de l'ensemble de données, il est difficile de visualiser et d'appliquer dans un sens réel. Trouver la variance n'est généralement que la dernière étape avant de trouver l'écart type. Les valeurs de variance sont parfois utilisées dans la finance et les formules statistiques.
L'écart-type, qui est exprimé dans les unités d'origine de l'ensemble de données, est beaucoup plus intuitive et plus proche des valeurs de l'ensemble de données d'origine. Il est le plus souvent utilisé pour analyser la démographie ou les échantillons de population pour avoir une idée de ce qui est normal dans la population.
Trouver des valeurs aberrantes
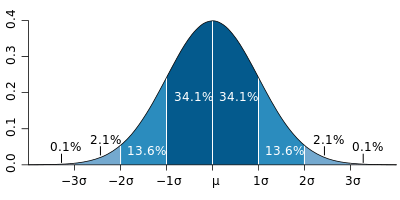 Une distribution normale (courbe de cloche) avec des bandes correspondant à 1σ
Une distribution normale (courbe de cloche) avec des bandes correspondant à 1σ Dans une distribution normale, environ 68% de la population (ou des valeurs) tombe dans un écart-type (1σ) de la moyenne et environ 94% tombent en 2σ. Des valeurs qui diffèrent de la moyenne de 1.7σ ou plus sont généralement considérés comme des valeurs aberrantes.
En pratique, des systèmes de qualité comme Six Sigma tentent de réduire le taux d'erreurs afin que les erreurs deviennent une valeur aberrante. Le terme «processus Six Sigma» provient de la notion que si l'on a six écarts-types entre la moyenne du processus et la limite de spécification la plus proche, pratiquement aucun élément ne manquera pas de spécifications.[1]
Échantillon d'écart type
Dans les applications du monde réel, les ensembles de données utilisés représentent généralement des échantillons de population, plutôt que des populations entières. Une formule légèrement modifiée est utilisée si des conclusions à l'échelle de la population doivent être tirées d'un échantillon partiel.
Un «échantillon d'écart-type» est utilisé si tout ce que vous avez est un échantillon, mais vous souhaitez faire une déclaration sur l'écart-type de la population à partir de laquelle l'échantillon est tiré
La seule façon dont la formule d'écart-type de l'échantillon diffère de la formule d'écart type est le «-1» du dénominateur.
En utilisant l'exemple de pissenlit, cette formule serait nécessaire si nous n'avions échantillon.
La somme des carrés serait désormais divisée par 5 au lieu de 6 (n - 1), ce qui donne une variance de 8.7 (au lieu de 7.25), et un échantillon d'écart type de 2.95 pouces, au lieu de 2.69 pouces pour l'écart type d'origine. Ce changement est utilisé pour trouver une marge d'erreur dans un échantillon (9% dans ce cas).